135° 120° 90°+

α
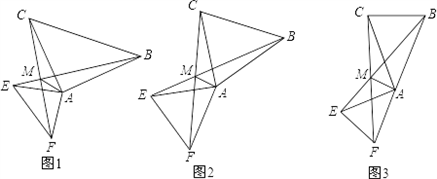
分析:①由∠BAC=∠EAF得∠FAC=∠EAB,并且AB=AC,AF=AE,∠BAC=∠EAF=90°,得到∠ACB=45°,易证△AFC≌△AEB,则∠ACF=∠ABE,则点A、B、C、M共圆,得到∠AMB=∠ACB=45°,于是得到∠AME=135°;
②同①一样,只是∠BAC=∠EAF=60°,得到∠ACB=60°,则∠AMB=∠ACB=60°,于是得到∠AME=120°;
③证明方法与①一样,∠AMB=∠ACB,∠BAC=∠EAF=α,则∠ACB=

(180°-α)=90°-

α,则∠AMB=90°-

α,根据平角的定义得到∠AME=180°-∠AMB,得到∠AME=90°+

α.
解答:①∵∠BAC=∠EAF,
∴∠FAC=∠EAB,
∵AB=AC,AF=AE,
∴△AFC≌△AEB,
∴∠ACF=∠ABE,
∴点A、B、C、M共圆,
∴∠AMB=∠ACB,
而∠BAC=90°,
∴∠ACB=45°,
∴∠AME=180°-45°=135°.
故答案为135°;
(2)与②证明方法一样得到∠AMB=∠ACB,
而∠BAC=60°,
∴∠ACB=60°,
∴∠AME=180°-60°=120°,
故答案为120°;
③∠AME=90°+

α.理由如下:
∵∠BAC=∠EAF=α,
∴∠FAC=∠EAB,
又∵AB=AC,AF=AE,
∴△AFC≌△AEB,
∴∠ACF=∠ABE,
∴点A、B、C、M共圆,
∴∠AMB=∠ACB,
∵AB=AC,∠BAC=α,
∴∠ACB=

(180°-α)=90°-

α,
∴∠AMB=90°-

α,
∴∠AME=180°-(90°-

α)=90°+

α.
点评:本题考查了全等三角形的判定与性质:有两组边对应相等,并且它们的夹角也相等的两三角形全等;全等三角形的对应角相等.也考查了等腰直角三角形的性质、等边三角形的性质以及四点共圆的判定与性质.

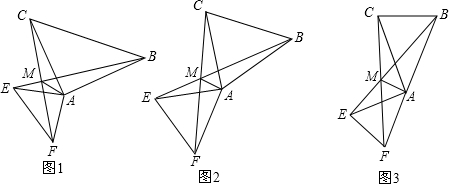
 α
α (180°-α)=90°-
(180°-α)=90°- α,则∠AMB=90°-
α,则∠AMB=90°- α,根据平角的定义得到∠AME=180°-∠AMB,得到∠AME=90°+
α,根据平角的定义得到∠AME=180°-∠AMB,得到∠AME=90°+ α.
α. α.理由如下:
α.理由如下: (180°-α)=90°-
(180°-α)=90°- α,
α, α,
α, α)=90°+
α)=90°+ α.
α.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案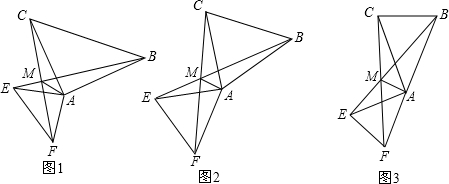
 已知如图△ABC和△DCE都为等边三角形,AE交CD于点N,BD交AC于点M.
已知如图△ABC和△DCE都为等边三角形,AE交CD于点N,BD交AC于点M.