

分析 (1)①利用同角的余角相等得出∠ABP=∠CPD,从而判断出结论;
②借助①的结论得出$\frac{AB}{DP}=\frac{AP}{DC}$,代入已知量,最后解方程即可得出结论;
(2)①同(1)①的方法判断出△ABP∽△DPQ,得出$\frac{AB}{DP}=\frac{AP}{DQ}$,再代换化简即可求出函数,用点Q在DC的延长线上得出y>0求出定义域即可;
②同(1)①的方法判断出△ABP∽△HPE,得出$\frac{AB}{PH}=\frac{AP}{HE}$,而PH=4-AP,HE=2,AB=2,HE=2,代入比例式即可求出AP
解答 解:(1)①如图1,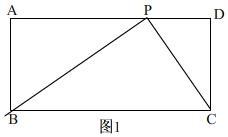 在矩形ABCD中,∠A=∠D=90°,
在矩形ABCD中,∠A=∠D=90°,
∴∠ABP+∠APB=90°,
∵∠BPC=90°,
∴∠APB+∠CPD=90°,
∴∠ABP=∠CPD,
∵∠A=∠D,
∴△ABP∽△DPC,
②由①知,△ABP∽△DPC,
∴$\frac{AB}{DP}=\frac{AP}{DC}$,
∵AB=CD=2,AD=5,
∴DP=AD-AP=5-AP,
∴$\frac{2}{5-AP}=\frac{AP}{2}$,
∴AP=1或AP=4,
(2)①如图2,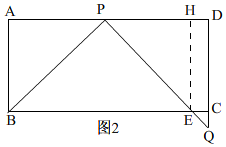
在矩形ABCD中,
同(1)①的方法得出△ABP∽△DPQ,
∴$\frac{AB}{DP}=\frac{AP}{DQ}$,
∵AB=CD=2,AD=5,CQ=y.AP=x,
∴DP=AD-AP=5-x,DQ=CD+CQ=2+y,
∴$\frac{2}{5-x}=\frac{x}{2+y}$,
∴y=-$\frac{1}{2}$(x2-5x+4)
∵y>0,
∴$\frac{1}{2}$(x2-5x+4)<0,
∴1<x<4
即:y=-$\frac{1}{2}$(x2-5x+4),定义域为1<x<4
②过点E作EH⊥AB,
∴DH=CE=1,HE=CD=2
∴AH=AD-DH=4,
∴PH=AH-AP=4-AP
同(1)①的方法得出,△ABP∽△HPE,
∴$\frac{AB}{PH}=\frac{AP}{HE}$,
∴$\frac{2}{4-AP}=\frac{AP}{2}$,
∴AP=2.
点评 此题是三角形综合题,主要考查了矩形的性质,相似三角形的性质和判定,同角的余角相等,解本题的关键是判断三角形相似.


科目:初中数学 来源: 题型:选择题
| A. | 10 cm | B. | 30 cm | C. | 50 cm | D. | 70 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$x+$\frac{1}{2}$y | B. | $\frac{1}{2}$x+$\frac{1}{3}$y | C. | x+$\frac{1}{3}$+$\frac{1}{2}$+y | D. | $\frac{1}{6}$(x+y) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,点O是∠ABC的平分线与线段BC的垂直平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB.垂足分别为D、E、F,则下列结论不一定成立的是( )
如图,在△ABC中,点O是∠ABC的平分线与线段BC的垂直平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB.垂足分别为D、E、F,则下列结论不一定成立的是( )| A. | OB=OC | B. | OD=OF | C. | OA=OB=OC | D. | BD=DC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
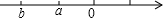 有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )
有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )| A. | a-b<0 | B. | a+b<0 | C. | a-b>0 | D. | $\frac{a}{b}$>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,如图是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”,…,照此规律,图A5比图A2多出“树枝”( )
如图所示,如图是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”,…,照此规律,图A5比图A2多出“树枝”( )| A. | 28 | B. | 56 | C. | 60 | D. | 124 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com