
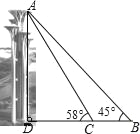
【题目】奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形![]() 置于平面直角坐标系
置于平面直角坐标系![]() 中,
中,![]() 在
在![]() 轴上,
轴上,![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,对角线
,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是第一象限内一点.
是第一象限内一点.
(1)如图1,若![]() ,
,![]() ,试判断四边形
,试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
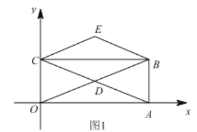
(2)如图2,当点![]() 使得
使得![]() 时,求证:
时,求证:![]() ;
;
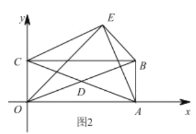
(3)在(2)的条件下,如果![]() 与
与![]() 恰好相等,求点
恰好相等,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
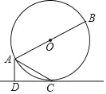
【题目】已知:如图,AB为⊙O的直径,AC是⊙O的弦,AD垂直于过点C的直线DC,垂足为点D,且AC平分∠BAD.
(1)求证:CD是⊙O的切线;
(2)若AD=1,AB=5,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技开发公司研制出一种新型产品,每件产品的成本为2400元,销售单价定为3000元.在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润最大,公司应将最低销售单价调整为多少元(其它销售条件不变)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选2名同学打第一场比赛,求下列事件的概率。
(1)已确定甲打第一场,再从其余3名同学中随机选取1名,恰好选中乙同学;
(2)随机选取2名同学,其中有乙同学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华商场销售某种冰箱,每台进价为2500元,销售价为2900元,平均每天能售出8台;调查发现,当销售价每降低50元,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱应该降价多少元?若设每台冰箱降价x元,根据题意可列方程( )
A. (2900-x)(8+4×![]() )=5000 B. (400-x)(8+4×
)=5000 B. (400-x)(8+4×![]() )=5000
)=5000
C. 4(2900-x)(8+![]() )=5000 D. 4(400-x)(8+
)=5000 D. 4(400-x)(8+![]() )=5000
)=5000
查看答案和解析>>
科目:初中数学 来源: 题型:
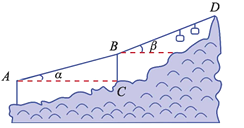
【题目】缆车,不仅提高了景点接待游客的能力,而且解决了登山困难者的难题.如图,当缆车经过点A到达点B时,它走过了700米.由B到达山顶D时,它又走过了700米.已知线路AB与水平线的夹角![]() 为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com