
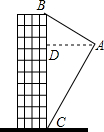
 如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88)
如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88) 分析 在Rt△ABD中,根据正切函数求得BD=AD•tan∠BAD,在Rt△ACD中,求得CD=AD•tan∠CAD,再根据BC=BD+CD,代入数据计算即可.
解答  解:如图,∵在Rt△ABD中,AD=54,∠BAD=32°,
解:如图,∵在Rt△ABD中,AD=54,∠BAD=32°,
∴BD=AD•tan32°≈54×0.625=33.75,
∵在Rt△ACD中,∠CAD=62°,
∴CD=AD•tan62°≈54×1.88=101.52,
∴BC=BD+CD≈33.75+101.52≈135.3.
答:该建筑物的高度BC约为135.3米.
点评 此题考查了解直角三角形的应用-仰角俯角问题.此题难度适中,注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
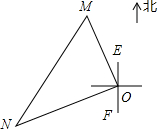 一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处.若M,N两点相距100海里,则∠NOF的度数为70°.
一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处.若M,N两点相距100海里,则∠NOF的度数为70°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
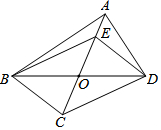 如图,在四边形ABCD中,对角线AC,BD相交于点O,且OB=OD.点E在线段OA上,连结BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是:①②或①④或②④(只填写序号).
如图,在四边形ABCD中,对角线AC,BD相交于点O,且OB=OD.点E在线段OA上,连结BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是:①②或①④或②④(只填写序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
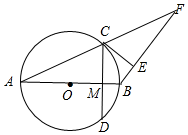 如图,以AB为直径的⊙O与AF交于C点,过C作CE⊥BF,且CE与⊙O相切,过C作CD⊥AB交AB于M,AB=10,OM:BM=3:2.
如图,以AB为直径的⊙O与AF交于C点,过C作CE⊥BF,且CE与⊙O相切,过C作CD⊥AB交AB于M,AB=10,OM:BM=3:2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com