解:(1)∵AB∥CD,
∴∠1+∠2=180°(两直线平行,同旁内角互补);

(2)过点E作一条直线EF平行于AB,
∵AB∥CD,
∵AB∥EF,CD∥EF,
∴∠1+∠AEF=180°,∠FEC+∠3=180°,
∴∠1+∠2+∠3=360°;
(3)过点E、F作EM、FN平行于AB,
∵AB∥CD,
∵AB∥EM∥FN∥CD,
∴∠1+∠AEM=180°,∠MEF+∠EFN=180°,∠NFC+∠4=180°;
∴∠1+∠2+3+∠4=540°;
(4)中,根据上述规律,显然作(n-1)条辅助线,运用(n-1)次两条直线平行,同旁内角互补.即可得到n个角的和是180°(n-1).
分析:(1)中,根据两条直线平行,同旁内角互补作答;
(2)过点E作平行于AB的直线,运用两次两条直线平行,同旁内角互补即可得到三个角的和;
(3)分别过点E,F作AB的平行线,运用三次平行线的性质,即可得到四个角的和;
(4)同样作辅助线,运用(n-1)次平行线的性质,则n个角的和是(n-1)180°.
点评:注意构造辅助线以及平行线的性质的运用.

 细观察,找规律
细观察,找规律


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案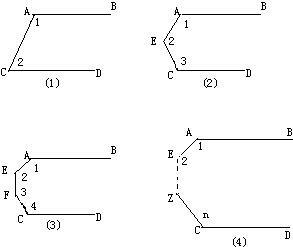 24、细观察,找规律
24、细观察,找规律