
 如图,平面直角坐标系xOy中,点C(3,0),函数y=$\frac{k}{x}$(k>0,x>0)的图象经过?OABC的顶点A(m,n)和边BC的中点D.
如图,平面直角坐标系xOy中,点C(3,0),函数y=$\frac{k}{x}$(k>0,x>0)的图象经过?OABC的顶点A(m,n)和边BC的中点D.分析 (1)根据平行四边形的性质确定出B的坐标从而确定出D的坐标,而点A,D在反比例函数图象上,建立方程求出m,
(2)根据三角形OAD的面积是平行四边形OABC面积的一半,确定出n即可;
(3)根据平行四边形的性质和双曲线的性质,确定出PM,ON即可.
解答 解:(1)∵点C(3,0),?OABC的顶点A(m,n),
∴B(m+3,n),
∴D($\frac{m}{2}$+3,$\frac{n}{2}$),
∵函数y=$\frac{k}{x}$(k>0,x>0)的图象经过?OABC的顶点A(m,n)和边BC的中点D,
∴mn=k,$\frac{n}{2}(\frac{m}{2}+3)=k$,
∴m=2,
(2)∵点D是平行四边形BC中点,
∴S平行四边形OABC=2S△OAD=12,
∵S平行四边形OABC=3×n=12,
∴n=4,
由(1)知,m=2,
∴k=mn=8,
(3)①如图1,点N在OA上,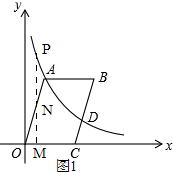
由(1)知,m=2,
∴A(2,n).
即0<t<2
直线OA的解析式为y=$\frac{n}{2}$x,
设点P的横坐标为t,
∴P(t,$\frac{2n}{t}$),
∵过点P作直线l⊥x轴于点M.
∴N(t,$\frac{n}{2}$t),M(t,0),
∴PN=$\frac{2n}{t}$-$\frac{n}{2}$t,PM=$\frac{2n}{t}$,
∵$\frac{PN}{PM}=\frac{1}{4}$,
∴$\frac{2n}{t}$=4($\frac{2n}{t}$-$\frac{n}{2}$t),
∴t=$\sqrt{3}$或t=-$\sqrt{3}$(舍),
②如图2,
当点N在AB上时,
由(1)知,B(5,n),
∴2≤t≤3
由题意知,P(t,$\frac{2n}{t}$).N(t,n),M(t,0),
∵$\frac{PN}{PM}=\frac{1}{4}$,
∴4(n-$\frac{2n}{t}$)=$\frac{2n}{t}$,
∴t=$\frac{5}{2}$,
③如图3,4,

当点N在BC上时,(3<t≤5)
∵B(5,n),C(3,0),
∴直线BC解析式为y=$\frac{n}{2}$x-$\frac{3n}{2}$,
∴P(t,$\frac{2n}{t}$),N(t,$\frac{n}{2}$t-$\frac{3n}{2}$),M(t,0),
∵$\frac{PN}{PM}=\frac{1}{4}$,
∴4|$\frac{n}{2}$t-$\frac{3n}{2}$-$\frac{2n}{t}$|=$\frac{2n}{t}$,
∴t=$\frac{3+\sqrt{29}}{2}$或t=$\frac{3-\sqrt{29}}{2}$(舍)或t=$\frac{3+\sqrt{21}}{2}$或t=$\frac{3-\sqrt{21}}{2}$(舍)
∴t的值为$\sqrt{3}$,$\frac{5}{2}$,$\frac{3+\sqrt{29}}{2}$或$\frac{3+\sqrt{21}}{2}$.
点评 此题是反比例函数综合题,主要考查了待定系数法,三角形的面积,平行四边形的面积,平行四边形的性质,解本题的关键是求出m,n的值.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:选择题
 如图,△ABC的周长为36cm,DE垂直平分边AC,交BC边于点E,交AC边于点D,连接AE,若AD=$\frac{15}{2}$cm,则△ABE的周长是( )
如图,△ABC的周长为36cm,DE垂直平分边AC,交BC边于点E,交AC边于点D,连接AE,若AD=$\frac{15}{2}$cm,则△ABE的周长是( )| A. | 22cm | B. | 20 cm | C. | 21cm | D. | 15cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届广东省佛山市顺德区九年级第一次模拟考试数学试卷(解析版) 题型:单选题
在Rt△ABC中,∠C=90°,sinA= ,AC=6cm,则BC的长度为( )
,AC=6cm,则BC的长度为( )
A. 6cm B. 7cm C. 8cm D. 9cm
查看答案和解析>>
科目:初中数学 来源:2017届湖北省九年级三月月考数学试卷(解析版) 题型:判断题
已知,A,B 两市相距 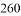 千米,甲车从 A 市前往 B 市运送物资,行驶
千米,甲车从 A 市前往 B 市运送物资,行驶  小时在 M 地汽车出现故障,立即通知技术人员乘乙车从 A 市赶来维修(通知时间忽略不计),乙车到达 M 地后又经过
小时在 M 地汽车出现故障,立即通知技术人员乘乙车从 A 市赶来维修(通知时间忽略不计),乙车到达 M 地后又经过  分钟修好甲车后以原速原路返回,同时甲车以原速
分钟修好甲车后以原速原路返回,同时甲车以原速 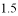 倍的速度前往 B 市,如图是两车距 A 市的路程
倍的速度前往 B 市,如图是两车距 A 市的路程  (千米)与甲车行驶时间
(千米)与甲车行驶时间  (小时)之间的函数图象,结合图象回答下列问题:
(小时)之间的函数图象,结合图象回答下列问题:
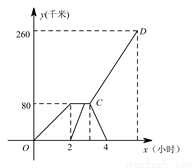
(1)直接写出甲车提速后的速度、乙车的速度、点  的坐标;
的坐标;
(2)求乙车返回时  与
与  的函数关系式并直接写出自变量
的函数关系式并直接写出自变量  的取值范围;
的取值范围;
(3)求甲车到达 B 市时乙车已返回 A 市多长时间?
查看答案和解析>>
科目:初中数学 来源:2017届湖北省九年级三月月考数学试卷(解析版) 题型:单选题
甲安装队为 A小区安装  台空调,乙安装队为 B小区安装
台空调,乙安装队为 B小区安装  台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装
台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装  台,设乙队每天安装
台,设乙队每天安装  台,根据题意,下面所列方程中正确的是
台,根据题意,下面所列方程中正确的是 
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com