

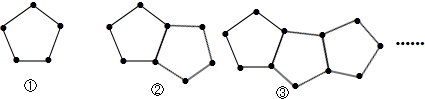
分析 (1)根据第一个图需棋子数是3×2,第二个图需棋子数是3×3,第三个图需棋子数是3×4,得出第5个图形有3×6个棋子,由此得出第n个图形有3(n+1)个棋子;
(2)设第n个图形有2013颗黑色棋子,根据(1)得出的规律,列出算式,求解即可.
解答 解:(1)∵第一个图需棋子数是:3×2=6个,
第二个图需棋子数是:3×3=9个,
第三个图需棋子数是:3×4=12个,
第四个图需棋子数是:3×5=15个,
∴第五个图需棋子数是:3×6=18个,
…
∴第n个图需棋子3(n+1)个.
(2)设第n个图形有2013颗黑色棋子,根据题意得:
3(n+1)=2013,
解得:n=670.
则第670个图形有2013颗黑色棋子.
点评 此题考查了图形的变化类,是一道关于数字猜想的问题,关键是通过归纳与总结,得到其中的规律;本题的规律是第n个图需棋子3(n+1)个.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
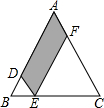 如图,在△ABC中,点D,E,F分别在边AB,BC,AC上,△DBE∽△FEC,3DE=CF.若S△ABC=48,则阴影部分的面积为18.
如图,在△ABC中,点D,E,F分别在边AB,BC,AC上,△DBE∽△FEC,3DE=CF.若S△ABC=48,则阴影部分的面积为18.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一条直线流水线上依次有5个机器人,它们站的位置在数轴上依次用点A1,A2,A3,A4,A5表示,如图:
一条直线流水线上依次有5个机器人,它们站的位置在数轴上依次用点A1,A2,A3,A4,A5表示,如图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com