解:(1)CE=BF.理由如下:
∵∠C=90°,
∴∠ACE+∠BCF=90°,
∵AE⊥l于E,BF⊥l于F,
∴∠AEC=∠BFC=90°,
∴∠EAC+∠ACE=90°,
∴∠EAC=∠BCF
∵AC=BC,
∴Rt△AEC≌Rt△CFB,
∴CE=BF;
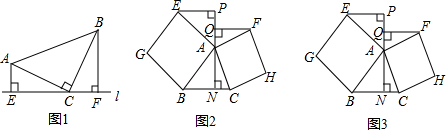
(2)EP=FQ.理由如下:
∵四边形ABGE和四边形ACHF都是正方形,
∴AE=AB,AF=AC,∠BAE=∠CAF=90°,
∵AN⊥BC于N,EP⊥AN于P,FQ⊥AN于Q,
∴∠ANC=∠ANB=∠EPA=∠FQA=90°,
∴∠EAP=∠ABN,∠FAQ=∠ACN,
∴Rt△FQA≌△ANC,△EPA≌△ANB,
∴FQ=AN,EP=AN,
∴EP=FQ;
(3)(2)中结论还成立,即EP=FQ;理由如下:
同(2)一样可得∠EAP=∠ABN,∠FAQ=∠ACN,
∴Rt△FQA∽△ANC,△EPA∽△ANB,
∴FQ:AN=AF:AC,EP:AN=AE:AB,
又∵GB=kAB,HC=kAC,
∴AF:AC=AE:AB=k,
∴FQ:AN=EP:AN,
∴EP=FQ.
分析:(1)易证Rt△AEC≌Rt△CFB,由全等三角形的性质可以得出结论CE=BF;
(2)由条件可以证明Rt△EQA≌Rt△ANC,可以得出FQ=AN,由Rt△EPQ≌Rt△ANB可以得出EP=AN,从而得出EP=FQ;
(3)由条件可以得出Rt△FQA∽Rt△ANC,Rt△EPA∽Rt△ANB,从而证明
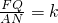
,

,从而得出EP=FQ.
点评:本题考查了相似三角形的判定与性质:有两组对应角分别相等的两三角形相似;相似三角形对应边的比相等.也考查了全等三角形的判定与性质以及正方形的性质.

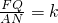 ,
, ,从而得出EP=FQ.
,从而得出EP=FQ.

 下列说法:
下列说法:


