
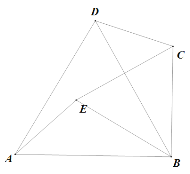
【题目】如图:两个等边三角形△ABD与△BCE,连结AE与CD,
求证:(1)AE=CD;
(2)AE与DC之间的夹角为60°;
(3)AE与CD的交点设为H,BH平分∠AHC.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)根据等边三角形的性质,易证△BCD≌△BEA,即可证得AE=CD;
(2)延长AE交CD于H,交BD于O,在△ODH和△AOB中,根据“8” 字形即可证明;
(3)过B作BM⊥CD于点M,过B作BN⊥AH于点N,证明△AMN≌△DBM,得出 BM=BN,即可通过角平分线的判定证明.
(1)∵等边三角形ABD和等边三角形BCE
∴∠ABD=∠CBE=60°,AB=BD,BE=BC,∠ABD-∠EBD=∠CBE-∠EBD,即∠ABE=∠DBC,
∴△BCD≌△BEA,
∴AE=DC
(2)延长AE交CD于H,交BD于O,在△ODH和△AOB中,
∵△BCD≌△BEA,
∴∠HDO=∠OAB,
又∵∠DOH=∠AOB,根据三角形内角和是180°,
∴∠DHO=∠ABO=60°

(3)过B作BM⊥CD交CD的延长线于点M,过B作BN⊥AH于点N,
∴∠BNA=∠BMD=90°,
∵△BCD≌△BEA,
∴AB=DB, ∠BAN=∠BDM
∴△AMN≌△DBM
∴BM=BN,
∴BH平分∠AHC.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=50°,P 为 AB 中点,点 M 为射线 AC 上(不与点 A 重合)的任意一点,连接 MP, 并使MP 的延长线交射线BD 于点N,设∠BPN=α.

(1)求证:△APM≌△BPN;
(2)当 MN=2BN 时,求α的度数;
(3)若△BPN 为锐角三角形时,直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D为射线BA上一点,连接DC,且DC=BC.
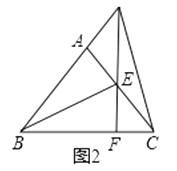
(1)如图1,若DC⊥AC,AB= ![]() ,求CD的长;
,求CD的长;
(2)如图2,若E为AC上一点,且CE=AD;连接BE,BE=2CE,连接DE并延长交BC于F.求证:DF=3EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.

(1)求证:△BCD是等腰三角形;
(2)△BCD的周长是a,BC=b,求△ACD的周长(用含a,b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小强进行百米赛跑,小明比小强跑得快,如果两人同时起跑,小明肯定赢,如图所示,现在小明让小强先跑_______米,直线__________表示小明的路程与时间的关系,大约_______秒时,小明追上了小强,小强在这次赛跑中的速度是________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
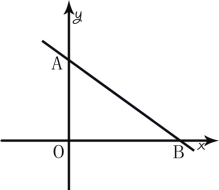
【题目】如图,直线MN与x轴、y轴分别相交于B、A两点,OA,OB的长满足式子![]()
(1)求A,B两点的坐标;
(2)若点O到AB的距离为![]() ,求线段AB的长;
,求线段AB的长;
(3)在(2)的条件下,x轴上是否存在点P,使ΔABP使以AB为腰的等腰三角形,若存在请直接写出满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AD与AB、CD交于A、D两点,EC、BF与AB、CD交于E、C、B、F,且∠1=∠2,∠B=∠C(如图).
(1)CE∥BF这一结论对吗?为什么?
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个几何体的主视图和左视图都是底边长为6,高为4的等腰三角形,俯视图是一个圆,那么这个几何体的侧面积是( ) 
A.12π
B.24π
C.![]() π
π
D.15π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com