
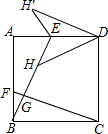
 如图,正方形ABCD的边长为3,点E、F分别在边AD、AB上且AE=BF=1,连接BE、CF交于点G,在线段EG上取一点H使HG=BG,连接DH,把△EDH沿AD边翻折得到△EDH’,则点H到边DH’的距离是$\frac{24}{25}\sqrt{5}$.
如图,正方形ABCD的边长为3,点E、F分别在边AD、AB上且AE=BF=1,连接BE、CF交于点G,在线段EG上取一点H使HG=BG,连接DH,把△EDH沿AD边翻折得到△EDH’,则点H到边DH’的距离是$\frac{24}{25}\sqrt{5}$. 分析 先连接HH',根据轴对称的性质,判定△ABE≌△BCF,再根据勾股定理求得CF=$\sqrt{10}$,BG=$\frac{3}{10}\sqrt{10}$,进而得出EH:HB=2:3,再根据平行线分线段成比例定理,求得PE=$\frac{2}{5}$,PH=$\frac{6}{5}$,PD=$\frac{12}{5}$,最后设点H到边DH'的距离是h,根据面积法得到$\frac{1}{2}$×HH'×PD=$\frac{1}{2}$×DH'×h,求得h的值即可.
解答 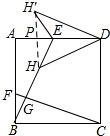 解:连接HH',交AD于P,则AD垂直平分HH',
解:连接HH',交AD于P,则AD垂直平分HH',
∴DH=DH',即△DHH'是等腰三角形,
∵正方形ABCD的边长为3,AE=BF=1,∠A=∠FBC=90°,
∴△ABE≌△BCF(SAS),
∴∠ABE=∠BCF,CF=BE,
又∵∠ABE+∠GBC=90°,
∴∠BCG+∠GBC=90°,
∴BG⊥CF,
∵BF=1,BC=3,
∴Rt△BCF中,CF=$\sqrt{10}$,BG=$\frac{3}{10}\sqrt{10}$,
∴HG=BG=$\frac{3}{10}\sqrt{10}$,
又∵CF=BE=$\sqrt{10}$,
∴HE=$\frac{4}{10}\sqrt{10}$,
∴EH:HB=2:3,
∵PH∥AB,
∴$\frac{PE}{AE}$=$\frac{PH}{AB}$=$\frac{2}{5}$,即$\frac{PE}{1}$=$\frac{PH}{3}$=$\frac{2}{5}$,
∴PE=$\frac{2}{5}$,PH=$\frac{6}{5}$,PD=$\frac{12}{5}$,
∴Rt△PDH中,DH=$\sqrt{(\frac{6}{5})^{2}+(\frac{2}{5}+2)^{2}}$=$\frac{6}{5}\sqrt{5}$=DH',HH'=2×$\frac{6}{5}$=$\frac{12}{5}$,
设点H到边DH'的距离是h,则
$\frac{1}{2}$×HH'×PD=$\frac{1}{2}$×DH'×h,
∴$\frac{12}{5}$×$\frac{12}{5}$=$\frac{6}{5}\sqrt{5}$×h,
∴h=$\frac{24}{25}\sqrt{5}$,
∴点H到边DH'的距离是$\frac{24}{25}\sqrt{5}$.
故答案为:$\frac{24}{25}\sqrt{5}$.
点评 本题以折叠问题为背景,主要考查了正方形的性质、勾股定理的应用、全等三角形的判定与性质的综合应用,解决问题的关键是根据面积法列出等式求得点H到边DH'的距离,解题时注意方程思想的运用.


科目:初中数学 来源: 题型:选择题
| A. | y=-2(x+3) | B. | y=-2(x-3) | C. | y=-2x+3 | D. | y=-2x-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.则每分出水( )
一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.则每分出水( )| A. | $\frac{15}{4}$升 | B. | 4升 | C. | 5升 | D. | $\frac{25}{4}$升 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com