
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 坐标为
坐标为![]() 、
、![]() ,
,![]() 为线段
为线段![]() 上的一点.
上的一点.
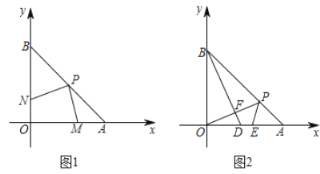
(1)如图1,若![]() 为
为![]() 的中点,点
的中点,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的动点,且保持
边上的动点,且保持![]() ,则在点
,则在点![]() 、
、![]() 运动的过程中,探究线段
运动的过程中,探究线段![]() 、
、![]() 之间的位置关系与数量关系,并说明理由.
之间的位置关系与数量关系,并说明理由.
(2)如图2,若![]() 为线段
为线段![]() 上异于
上异于![]() 、
、![]() 的任意一点,过
的任意一点,过![]() 点作
点作![]() ,交
,交![]() 、
、![]() 分别于
分别于![]() 、
、![]() 两点,
两点,![]() 为
为![]() 上一点,且
上一点,且![]() ,试判断线段
,试判断线段![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)PM=PN,PM⊥PN,理由见解析;(2)OD=AE,理由见解析
【解析】
(1)连接OP.只要证明△PON≌△PAM即可解决问题;
(2)作AG⊥x轴交OP的延长线于G.由△DBO≌△GOA,推出OD=AG,∠BDO=∠G,再证明△PAE≌△PAG即可解决问题;
(1)结论:PM=PN,PM⊥PN.理由如下:
如图1中,连接OP.
∵A、B坐标为(6,0)、(0,6),
∴OB=OA=6,∠AOB=90°,
∵P为AB的中点,
∴OP=![]() AB=PB=PA,OP⊥AB,∠PON=∠PAM=45°,
AB=PB=PA,OP⊥AB,∠PON=∠PAM=45°,
∴∠OPA=90°,
在△PON和△PAM中,
 ,
,
∴△PON≌△PAM(SAS),
∴PN=PM,∠OPN=∠APM,
∴∠NPM=∠OPA=90°,
∴PM⊥PN,PM=PN.
(2)结论:OD=AE.理由如下:
如图2中,作AG⊥x轴交OP的延长线于G.
∵BD⊥OP,
∴∠OAG=∠BOD=∠OFD=90°,
∴∠ODF+∠AOG=90°,∠ODF+∠OBD=90°,
∴∠AOG=∠DBO,
∵OB=OA,
∴△DBO≌△GOA,
∴OD=AG,∠BDO=∠G,
∵∠BDO=∠PEA,
∴∠G=∠AEP,
在△PAE和△PAG中,
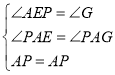 ,
,
∴△PAE≌△PAG(AAS),
∴AE=AG,
∴OD=AE.


科目:初中数学 来源: 题型:
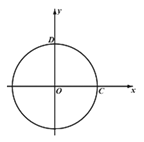
【题目】如图,在平面直角坐标系xOy中,一次函数y=-![]() +b(b>0,b为常数)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴交于点C,与y轴正半轴相交于点D.
+b(b>0,b为常数)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴交于点C,与y轴正半轴相交于点D.
(1)若直线AB与⊙O相切于弧CD上一点,求b的值;
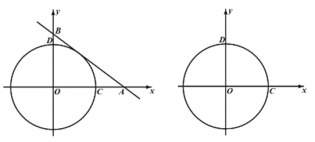
(2)若直线AB与⊙O有两个交点F、G.
①b为何值时,⊙O上有且只有3个点到直线AB的距离为2?并求出此时直线被⊙O所截的弦FG的长;
②是否存在这样的b,使得∠GOF=90°?若存在,求出b的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )

A.①②B.②③C.①③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,以其三边为直径向三角形外作三个半圆,矩形EFGH的各边分别与半圆相切且平行于AB或BC,则矩形EFGH的周长是 .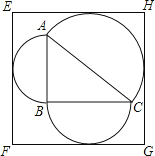
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点。

(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法)。
①作∠DAC的平分线AM。②连接BE并延长交AM于点F。
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)该商店销售这种电子鞭炮要想每天获得2400元的销售利润,又想买得快.那么销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com