
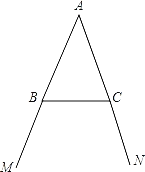
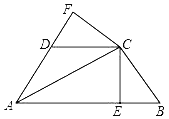
【题目】如图,AM=AN,点B和点C分别为∠MAN两边上的点,AB=AC.按下列语句画出图形:(要求用无刻度直尺作图,)
(1)AD⊥BC,垂足为D;
(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形:
【答案】(1)见解析;(2)△ACM≌△ABN,△ABT≌△ACT,△BMT≌△CNT,△AMT≌△ANT,△BDT≌△CDT,△BCM≌△CBN(任选其二即可).
【解析】
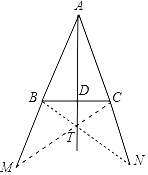
(1)连接BN和CM交于点T,连接AT交BC于D,AD即为所求;
(2)根据全等三角形的判定定理,逐一分析即可.
解:(1)连接BN和CM交于点T,连接AT交BC于D,AD即为所求
理由如下:
在△ACM和△ABN中
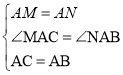
∴△ACM≌△ABN
∴∠M=∠N
∵BM=AM-AB=AN-AC=CN
在△BMT和△CNT中
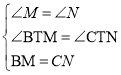
∴△BMT≌△CNT
∴TB=TC
∴T在BC中垂线上,
∵AB=AC
∴A也在BC中垂线上
根据两点确定一条直线
∴AT垂直平分BC
∴AD⊥BC
(2)△ACM≌△ABN,△ABT≌△ACT,△BMT≌△CNT,△AMT≌△ANT,△BDT≌△CDT,△BCM≌△CBN(任选其二即可).


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a-2b+c<0.其中正确的有( )

A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (a>0,a为常数)和y=
(a>0,a为常数)和y=![]() 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=![]() 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y=![]() 图象于点A;MD⊥y轴于点D,交y=
图象于点A;MD⊥y轴于点D,交y=![]() 的图象于点B,当点M在y=
的图象于点B,当点M在y=![]() 的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是___________;
的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是___________;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)在图中的点上标出相应字母A、B、C,并求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
(1)求证:△BCE≌△DCF;
(2)若AB=21,AD=9,BC=CD=10,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形![]() 中,对角线
中,对角线![]() ,
,![]() 相交于点
相交于点![]() ,若
,若![]() 、
、![]() 是
是![]() 上两动点,
上两动点,![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时以
两点同时以![]() 的相同的速度向
的相同的速度向![]() 、
、![]() 运动
运动

![]() 四边形
四边形![]() 是平行四边形吗?说明你的理由.
是平行四边形吗?说明你的理由.
![]() 若
若![]() ,
,![]() ,当运动时间
,当运动时间![]() 为多少时,以
为多少时,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为矩形.
为顶点的四边形为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠A=∠B=30°,E,F 在 AB 上,∠ECF=60°.
(1)画出△BCF 绕点 C 顺时针旋转 120°后的△ACK;
(2)在(1)中,若 AE2+ EF2= BF2,求证 BF=![]() CF.
CF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;

(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com