
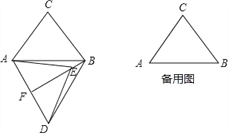
����Ŀ���ڡ�ABC��,AB=6,AC=BC=5,����ABC�Ƶ�A��˳ʱ�뷽����ת,�õ���ADE,��ת��Ϊ����0�㣼����180�㣩,��B�Ķ�Ӧ��Ϊ��D,��C�Ķ�Ӧ��Ϊ��E,����BD��BE��
��1����ͼ,����=60��ʱ,�ӳ�BE��AD�ڵ�F��
����֤����ABD�ǵȱ������Σ�
����֤��BF��AD��AF=DF��
����ֱ��д��BE�ij���
��2������ת������,����D��DG��ֱ��ֱ��AB,����Ϊ��G,����CE,����DAG=��ACB,���߶�DG���߶�AE������ʱ,��ֱ��д��BE+CE��ֵ��
���𰸡���1���٢������������3![]() ��4����2��13��
��4����2��13��
�������������������1��������ת����֪AB=AD����BAD=60�����ɵ�֤������BA=BD��EA=ED�����д������ʼ��ɵ�֤�����ֱ����BF��EF�ij����ɵã���2������ACB+��BAC+��ABC=180������DAG+��DAE+��BAE=180������DAG=��ACB����DAE=��BAC����BAE=��BAC��AE=AC���������ߺ�һ�ɵ�CE��AB��AC=5��AH=3���̶�֪CE=2CH=8��BE=5�����ɵô𰸣�
�����������1���١ߡ�ABC�Ƶ�A˳ʱ�뷽����ת60���õ���ADE��
��AB=AD����BAD=60����
���ABD�ǵȱ������Σ�
����������ABD�ǵȱ������Σ�
��AB=BD��
�ߡ�ABC�Ƶ�A˳ʱ�뷽����ת60���õ���ADE��
��AC=AE��BC=DE��
����AC=BC��
��EA=ED��
����B��E��AD���д����ϣ�
��BE��AD���д��ߣ�
����F��BE���ӳ����ϣ�
��BF��AD�� AF=DF��
������֪BF��AD��AF=DF��
��AF=DF=3��
��AE=AC=5��
��EF=4��
���ڵȱ�������ABD�У�BF=ABsin��BAF=6��![]() =3
=3![]() ��
��
��BE=BF��EF=3![]() ��4��
��4��
��2����ͼ��ʾ��
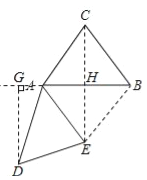
�ߡ�DAG=��ACB����DAE=��BAC��
���ACB+��BAC+��ABC=��DAG+��DAE+��ABC=180����
���ߡ�DAG+��DAE+��BAE=180����
���BAE=��ABC��
��AC=BC=AE��
���BAC=��ABC��
���BAE=��BAC��
��AB��CE����CH=HE=![]() CE��
CE��
��AC=BC��
��AH=BH=![]() AB=3��
AB=3��
��CE=2CH=8��BE=5��
��BE+CE=13��


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ÿһ���ڽǶ�����150�㣬��Ӵ˶����һ�����㷢���ĶԽ����У� ��
A.7��
B.8��
C.9��
D.10��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��a��b��c��ͬһƽ������������ֱ�������������(����)
A. 1����2����3�� B. 0����1����2����3��
C. 1����2�� D. ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ε�������λ�ߵij�Ϊ6��7��8����������ε��ܳ�Ϊ��������
A. 40B. 41C. 42D. 43
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
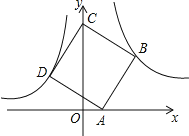
����Ŀ����ͼ����B��3��3����˫����y=![]() ��x��0���ϣ���D��˫����y=��
��x��0���ϣ���D��˫����y=��![]() ��x��0���ϣ���A�͵�C�ֱ���x�ᡢy����������ϣ��ҵ�A��B��C���ɵ��ı���Ϊ������
��x��0���ϣ���A�͵�C�ֱ���x�ᡢy����������ϣ��ҵ�A��B��C���ɵ��ı���Ϊ������
��1����k��ֵ��
��2�����A�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OCDE�Ķ���C��E�ֱ���y����������x����������ϣ�OC=8��OE=17��������y=![]() x2��3x+m��y���ཻ�ڵ�A�������ߵĶԳ�����x���ཻ�ڵ�B����CD���ڵ�K��
x2��3x+m��y���ཻ�ڵ�A�������ߵĶԳ�����x���ཻ�ڵ�B����CD���ڵ�K��
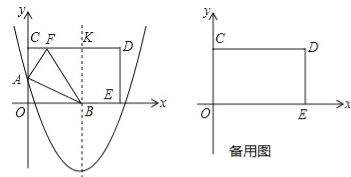
��1��������OCDE��AB�۵�����Oǡ�����ڱ�CD�ϵĵ�F����
����B�������� �� ����BK�ij��� ��CK�ij��� ��
�����F�����ꣻ
����ֱ��д�������ߵĺ�������ʽ��
��2��������OCDE���ž�����E��ֱ���۵�����Oǡ�����ڱ�CD�ϵĵ�G��������OG���ۺ���OG�ཻ�ڵ�H����M���߶�EH�ϵ�һ�����㣨�����H�غϣ�������MG��MO������G��GP��OM�ڵ�P����EH�ڵ�N������ON����M�ӵ�E��ʼ���߶�EH���H�˶��������N�غ�ʱֹͣ����MOG����NOG������ֱ��ʾΪS1��S2���ڵ�M���˶������У�S1S2����S1��S2�Ļ�����ֵ�Ƿ����仯�����仯����ֱ��д���仯��Χ�������䣬��ֱ��д�����ֵ��
��ܰ��ʾ���������Ը������⣬�ڱ���ͼ�в���ͼ�Σ��Ա�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x2+mxy+4y2����ȫƽ��ʽ������m��ֵΪ��������
A. 4 B. ��4
C. ��4 D. ���Ͻ��������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com