
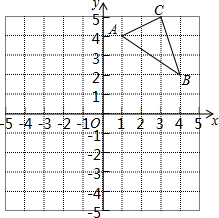
 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).分析 (1)根据网格特点,找出点A、B、C关于x轴的对称点A1、B1、C1的位置,然后顺次连接即可;
(2)分别找出点A、B、C绕点O逆时针旋转90°的对应点A2、B2、C2的位置,然后顺次连接即可,观察可知点B所经过的路线是半径为$\sqrt{{4}^{2}+{2}^{2}}$,圆心角是90°的扇形,然后根据弧长公式进行计算即可求解.
解答 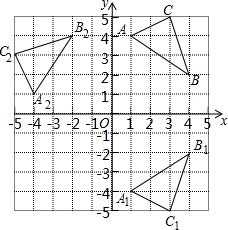 解:(1)如图,△A1B1C1即为所求.
解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
点B旋转到点B2所经过的路径长为:$\frac{90π\sqrt{{4}^{2}+{2}^{2}}}{180}$=$\sqrt{5}$π.
故点B旋转到点B2所经过的路径长是$\sqrt{5}$π.
点评 本题综合考查了利用对称变换作图,利用旋转变化作图,熟知网格结构特点找出变换后的对应点的位置是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1厘米,AB=3厘米,BC=5厘米,动点P从点B出发以1厘米/秒的速度沿BC方向运动,动点Q从点C出发以2厘米/秒的速度沿CD方向运动,P,Q两点同时出发,当点Q到达点D时停止运动,点P也随之停止,设运动时间为t秒(t>0).
如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1厘米,AB=3厘米,BC=5厘米,动点P从点B出发以1厘米/秒的速度沿BC方向运动,动点Q从点C出发以2厘米/秒的速度沿CD方向运动,P,Q两点同时出发,当点Q到达点D时停止运动,点P也随之停止,设运动时间为t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示;△ABC是等腰三角形,∠ABC=90°.
如图所示;△ABC是等腰三角形,∠ABC=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,这是某校初三年级同学们最喜爱的一项课外运动调查结果扇形图,但负责画此图的同学忘记了最喜爱篮球运动的人数.
如图,这是某校初三年级同学们最喜爱的一项课外运动调查结果扇形图,但负责画此图的同学忘记了最喜爱篮球运动的人数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.
如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com