
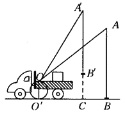
【题目】小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至 A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊绳A′B′=AB.AB垂直地面 O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA![]() ,sinA′
,sinA′![]() .求此重物在水平方向移动的距离BC.
.求此重物在水平方向移动的距离BC.
 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,PQ、PB、QC是⊙O的切线,切点分别为A、B、C,点D在![]() 上,若∠D=100°,则∠P与∠Q的度数之和是( )
上,若∠D=100°,则∠P与∠Q的度数之和是( )
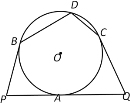
A.160°B.140°C.120°D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AEAD=AHAF;其中结论正确的个数是( )
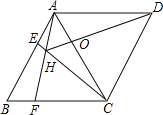
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知在四边形ABCD中,![]() ,
,![]() ,
,![]() ,动点P从点B出发沿折线B→A→D→C的方向以1个单位/秒的速度匀速运动,整个运动过程中,△BCP的面积S与运动时间t(秒)的函数关系如图2所示,则AD的长为( )
,动点P从点B出发沿折线B→A→D→C的方向以1个单位/秒的速度匀速运动,整个运动过程中,△BCP的面积S与运动时间t(秒)的函数关系如图2所示,则AD的长为( )
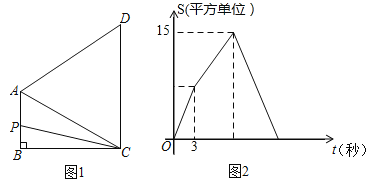
A.5B.![]() C.8D.
C.8D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
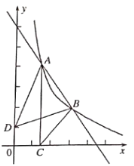
【题目】如图,点![]() 、
、![]() 是直线
是直线![]() 与反比例函数
与反比例函数![]() 图象的两个交点,
图象的两个交点,![]() 轴于点C,己知点D(0,1),连接AD、BD、BC,
轴于点C,己知点D(0,1),连接AD、BD、BC,
(1)求反比例函数和直线AB的表达式;
(2)根据函数图象直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)设△ABC和△ABD的面积分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=90°,点D在线段BC上,∠EDB=![]() ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
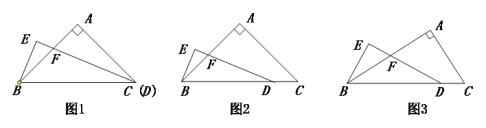
探究:当AB=AC且C,D两点重合时(如图1)探究:
(1)线段BE与FD之间的数量关系,直接写出结果 ;
(2)∠EBF= .
证明:当AB=AC且C,D不重合时,探究线段BE与FD的数量关系,并加以证明.
计算:当AB=![]() AC时,如图,求
AC时,如图,求![]() 的值 (用含
的值 (用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处.
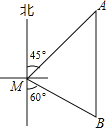
(1)求渔船从A到B的航行过程中与小岛M之间的最小距离(结果用根号表示):
(2)若渔船以20海里/小时的速度从B沿BM方向行驶,求渔船从B到达小岛M的航行时间(结果精确到0.1小时).(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.


(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com