
如图,正比例函数y1=x的图象与反比例函数 (k≠0)的图象相交于A、B两点,点A的纵坐标为2.
(k≠0)的图象相交于A、B两点,点A的纵坐标为2.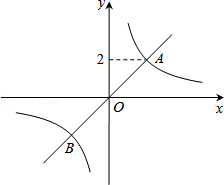
(1)求反比例函数的解析式;
(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量x的取值范围.
(1)
(2点B的坐标为(﹣2,﹣2)。
﹣2<x<0或x>2。
解析试题分析:(1)设A(m,2),将A纵坐标代入正比例解析式求出m的值,确定出A坐标,代入反比例解析式求出k的值,即可确定出反比例解析式。
(2)联立两函数解析式求出B的坐标,由A与B横坐标,利用图象即可求出当y1>y2时,自变量x的取值范围。
解:(1)设A点的坐标为(m,2),代入y1=x得:m=2,
∴点A的坐标为(2,2)。
代入 得:k=2×2=4。
得:k=2×2=4。
∴反比例函数的解析式为 。
。
(2)当y1=y2时, ,解得:x=±2,
,解得:x=±2,
∴点B的坐标为(﹣2,﹣2)。
∴由图象可知,当y1>y2时,自变量x的取值范围是:﹣2<x<0或x>2。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
已知平面直角坐标系xOy(如图),直线 经过第一、二、三象限,与y轴交于点B,点A(2,t)在这条直线上,连接AO,△AOB的面积等于1.
经过第一、二、三象限,与y轴交于点B,点A(2,t)在这条直线上,连接AO,△AOB的面积等于1.
(1)求b的值;
(2)如果反比例函数 (
( 是常量,
是常量, )的图像经过点A,求这个反比例函数的解析式.
)的图像经过点A,求这个反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线l:y=x+1与x轴、y轴分别交于A、B两点,点C与原点O关于直线l对称.反比例函数 的图象经过点C,点P在反比例函数图象上且位于C点左侧,过点P作x轴、y轴的垂线分别交直线l于M、N两点.
的图象经过点C,点P在反比例函数图象上且位于C点左侧,过点P作x轴、y轴的垂线分别交直线l于M、N两点.
(1)求反比例函数的解析式;
(2)求AN•BM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,一次函数y=kx+b与反比例函数 的图象交于点A,与x轴交于点B,AC⊥x轴于点C,
的图象交于点A,与x轴交于点B,AC⊥x轴于点C, ,AB=
,AB=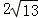 ,OB=OC.
,OB=OC.
(1)求反比例函数和一次函数的解析式;
(2)若一次函数与反比例函数的图象的另一交点为D,作DE⊥y轴于点E,连接OD,求△DOE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),反比例函数的图象经过点C.
(1)求点C的坐标及反比例函数的解析式.
(2)将等边△ABC向上平移n个单位,使点B恰好落在双曲线上,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,点A(m,m+1),B(m+1,2m-3)都在反比例函数 的图象上.
的图象上.
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点, 以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,上下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两全等的矩形,如果用彩色胶带如图包扎礼盒,所需胶带长度至少为__________cm.(不计接缝,结果保留准确值)
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,OP∥QR∥ST,则下列各式中正确的是( )
| A.∠1+∠2+∠3=180° | B.∠1+∠2﹣∠3=90° |
| C.∠1﹣∠2+∠3=90° | D.∠2+∠3﹣∠1=180° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com