
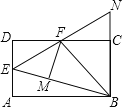
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是( )
A. ①②③
B. ①②④
C. ②③④
D. ①②③④
【答案】B
【解析】试题分析:∵四边形ABCD是矩形,∴∠D=∠BCD=90°,由折叠的性质可得:∠EMF=∠D=90°,DF=MF,
即FM⊥BE,CF⊥BC, ∵BF平分∠EBC, ∴CF=MF, ∴DF=CF;故①正确;
∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF, ∴∠BFM=∠BFC, ∵∠MFE=∠DFE=∠CFN,
∴∠BFE=∠BFN, ∵∠BFE+∠BFN=180°, ∴∠BFE=90°, 即BF⊥EN,故②正确;
∵在△DEF和△CNF中,∠D=∠FCN=90°,DF=CF,∠DFE=∠CFN∴△DEF≌△CNF(ASA),
∴EF=FN, ∴BE=BN, 但无法求得△BEN各角的度数, ∴△BEN不一定是等边三角形;故③错误;
∵∠BFM=∠BFC,BM⊥FM,BC⊥CF, ∴BM=BC=AD=2DE=2EM, ∴BE=3EM,
∴S△BEF=3S△EMF=3S△DEF;∴④正确.


科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣ ![]() ×(0.5﹣
×(0.5﹣ ![]() )÷(﹣
)÷(﹣ ![]() )
)
(2)﹣22﹣[(﹣3)×(﹣ ![]() )﹣(﹣2)3]
)﹣(﹣2)3]
(3)当x=2,y= ![]() 时,化简求值:
时,化简求值: ![]() x﹣(﹣
x﹣(﹣ ![]() )﹣(2x﹣
)﹣(2x﹣ ![]() y2)
y2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震发生后,全国人民抗震救灾,众志成城,在地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表,则当y<5时,x的取值范围是_____.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 10 | 5 | 2 | 1 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
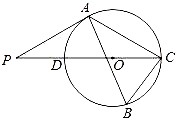
(1)求证:PA是⊙O的切线;
(2)若⊙O的半径为3,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com