
分析 (1)根据数的算术平方根的计算可以求出(1)中各数的值.
(2)从(1)中可以得到规律正数的平方的算术平方根为其本身,负数的平方的算术平方根为其相反数.0的算术平方根为其本身.
解答 解:(1)①$\sqrt{{3}^{2}}$=$\sqrt{9}$=3;$②\sqrt{{0.5}^{2}}$=0.5; $③\sqrt{{(-6)}^{2}}$=$\sqrt{36}$=6;
④$\sqrt{{0}^{2}}$=0;⑤$\sqrt{{(-\frac{3}{4})}^{2}}$=$\frac{3}{4}$;⑥$\sqrt{{(-\frac{1}{3})}^{2}}$=$\frac{1}{3}$
故答案为:3;0.5;6;0;$\frac{3}{4}$;$\frac{1}{3}$;
(2)$\sqrt{{a}^{2}}$不一定等于a,
当a<0时,$\sqrt{{a}^{2}}$=-a;
当a≥0时,$\sqrt{{a}^{2}}$=a;
故$\sqrt{{a}^{2}}$不一定等于a;
从中可以得到规律:正数和零的平方的算术平方根为其本身,负数的平方的算术平方根为其相反数.
点评 本题首先考查了正数的平方的算术平方根的规律,会总结和应用题目中数字变化的规律是解答此题的关键.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
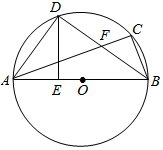 如图,△ABC内接于⊙O,AB为直径,点D是$\widehat{AC}$上一点,且∠DAC=∠DBA,过点D作DE⊥AB,垂足为点E,连结AD.
如图,△ABC内接于⊙O,AB为直径,点D是$\widehat{AC}$上一点,且∠DAC=∠DBA,过点D作DE⊥AB,垂足为点E,连结AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
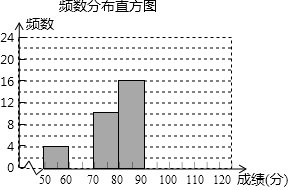 2017年3月在北京市召开的第十二届全国人民代表大会第五次会议上,环境问题再次成为大家讨论的重点内容之一.2017年6月5日是世界环境日,为纪念第46个世界环境日,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了50名学生的成绩进行统计分析,经分组整理后绘制成频数分布表和频数分布直方图.
2017年3月在北京市召开的第十二届全国人民代表大会第五次会议上,环境问题再次成为大家讨论的重点内容之一.2017年6月5日是世界环境日,为纪念第46个世界环境日,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了50名学生的成绩进行统计分析,经分组整理后绘制成频数分布表和频数分布直方图.| 分组/分 | 频数 | 频率 |
| 50~60 | 4 | 0.08 |
| 60~70 | a | 0.16 |
| 70~80 | 10 | 0.20 |
| 80~90 | 16 | 0.32 |
| 90~100 | b | c |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com