
【题目】园林部门用3600盆甲种花卉和2900盆乙种花卉搭配A、B两种园艺造型共50个,挂放在迎宾大道两侧,搭配每个造型所要花盆数如表,综合上述信息,解答下列问题.
造型 | 甲 | 乙 |
A | 90盆 | 30盆 |
B | 40盆 | 100盆 |
(1)符合题意的搭配方案有哪几种?
(2)若搭配一个A种造型的成本为1000元,搭配一个乙种造型的成本为1200元,选(1)中那种方案的成本最低?
【答案】
(1)解:设需要搭配x个A种造型,则需要搭配B种造型(50﹣x)个,
则有 ![]() ,
,
解得30≤x≤32,
所以x=30或31或32.
第一方案:A种造型32个,B种造型18个;
第二种方案:A种造型31个,B种造型19个;
第三种方案:A种造型30个,B种造型20个.
(2)解:总成本为:1000x+1200(50﹣x)=60000﹣2x.
显然当x取最大值32时成本最低,为60000﹣2×32=53600
答:第一种方案成本最低,最低成本是53600
【解析】①根据题意列出不等式组设需要搭配x个A种造型,则需要搭配B种造型(50﹣x)个,得到不等式组90x+40(50x)≤3600,30x+100(50x)≤2900;得出三种可能性;②根据总成本为1000x+1200(50﹣x)=60000﹣2x,显然当x取最大值32时成本最低,为60000﹣2×32=53600.
【考点精析】解答此题的关键在于理解一元一次不等式组的应用的相关知识,掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.


科目:初中数学 来源: 题型:
【题目】如图所示,已知∠A=∠F,∠C=∠D,按图填空,并在括号内注明理由.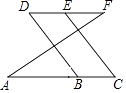
∵∠A=∠F()
∴∥()
∴∠D=∠ABD()
又∵∠D=∠C()
∴∠C=∠ABD()
∴∥()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:直线y1=﹣2x+3和直线y2=mx﹣1分别交y轴于点A、B,两直线交于点C(1,n). 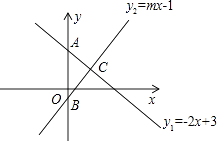
(1)求m,n的值.
(2)求△ABC的面积.
(3)请根据图象直接写出:当y1<y2时,向变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2,0),线段OA的长为6.将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处.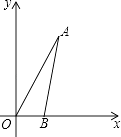
(1)请在图中画出△COD;
(2)求点A旋转过程中所经过的路程(精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展社会实践大课堂活动,七年级学生8点钟从学校乘大客车去博物馆参观.小明同学由于在去学校的路上遇到了堵车情况,8:10才到学校,他的家长立刻开汽车从学校出发,沿相同的路线送小明追赶大客车,结果8:30追上了大客车.已知小明家长的汽车的速度比大客车的速度每小时多29千米,求大客车的速度是每小时多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com