
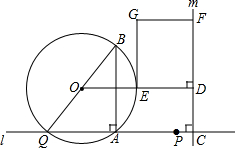
 ��ͼ����A�Ͷ���P��ֱ��l�ϣ���P���ڵ�A�ĶԳƵ�ΪQ����AQΪ����Rt��ABQ��ʹ��BAQ=90�㣬AQ��AB=3��4������ABQ�����ԲO����C�ڵ�P�Ҳ࣬PC=4������C��ֱ��m��l������O��OD��m�ڵ�D����AB�Ҳ��Բ���ڵ�E��������CD��ȡ��F��ʹDF=$\frac{3}{2}$CD����DE��DFΪ�ڱ�������DEGF����AQ=3x
��ͼ����A�Ͷ���P��ֱ��l�ϣ���P���ڵ�A�ĶԳƵ�ΪQ����AQΪ����Rt��ABQ��ʹ��BAQ=90�㣬AQ��AB=3��4������ABQ�����ԲO����C�ڵ�P�Ҳ࣬PC=4������C��ֱ��m��l������O��OD��m�ڵ�D����AB�Ҳ��Բ���ڵ�E��������CD��ȡ��F��ʹDF=$\frac{3}{2}$CD����DE��DFΪ�ڱ�������DEGF����AQ=3x���� ��1����AQ��AB=3��4��AQ=3x����AB=4x���ɹ��ɶ�����BQ��������λ�ߵ����ʵ�AH=BH=$\frac{1}{2}$AB�����BQ��FD��
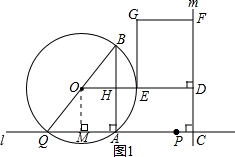
��2�����ã�1���Ľ��ۣ���CQ�ij�����OM��AQ�ڵ�M����ͼ1������OM��AB���ɴ���������QM=AM=x���ɾ������ʵ�OD=MC��������þ��������
��3����Ҫ�������ۣ�����ͼ1����P�ڵ�A���Ҳࣻ��P�ڵ�A�����ʱ���ٵ���C�ڵ�Q���Ҳ�ʱ����0��x��$\frac{4}{7}$ʱ������ͼ3��$\frac{4}{7}$��x��$\frac{2}{3}$ʱ���۵���C�ڵ�Q�����ʱ����ͼ4��$x��\frac{2}{3}$ʱ���Բ�������ʽ���н�ɣ�
���  ��1���⣺��Rt��ABQ�У�
��1���⣺��Rt��ABQ�У�
��AQ��AB=3��4��AQ=3x��
��AB=4x��
��BQ=5x��
��OD��m��m��l��
��OD��l��
��OB=OQ��
��AH=BH=$\frac{1}{2}$AB=2x��
��CD=2x��
��FD=$\frac{3}{2}$CD=3x��
����������BQ=5x��DF=3x��
��2����AP=AQ=3x��PC=4��
��CQ=6x+4��
��ͼ1������O��OM��AQ�ڵ�M��
��OM��AB��
�ߡ�O�ǡ�ABQ�����Բ����BAQ=90�㣬
���O��BQ���е㣬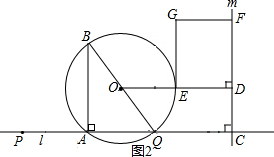
��QM=AM=$\frac{3}{2}x$
��OD=MC=$\frac{9}{2}x+4$��
��OE=$\frac{1}{2}$BQ=$\frac{5}{2}x$
��ED=2x+4
��S����DEGF=DF•DE=3x��2x+4��=90��
���x1=3��x2=-5����ȥ����
��${S_{��O}}=\frac{225��}{4}$��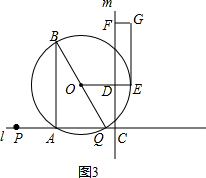
��3��������DEGF����������ED=FD
����ͼ1����P�ڵ�A���Ҳ�ʱ��
��2x+4=3x���x=4
��S��O=100��
��P�ڵ�A�����ʱ��
�ٵ���C�ڵ�Q���Ҳ�ʱ��
��ͼ2��0��x��$\frac{4}{7}$ʱ��
��ED=4-7x��FD=3x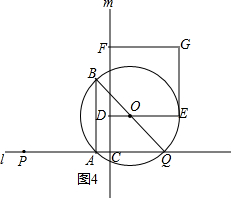
��4-7x=3x���$x=\frac{2}{5}$
��S��O=��
����ͼ3��$\frac{4}{7}$��x��$\frac{2}{3}$ʱ��
��ED=7-4x��FD=3x
��7-4x=3x���x=1����ȥ����
�۵���C�ڵ�Q�����ʱ����ͼ4��$x��\frac{2}{3}$
��DE=7x-4��FD=3x��
����7x-4=3x���x=1��
��${S_{��O}}=\frac{25��}{4}$��
��S��O=100�л�л�$\frac{25��}{4}$��
���� ������Ҫ������Բ���ۺ��⣮��Ҫ���չ��ɶ��������������������ε����ʣ���λ�ߵ����ʵȣ����ͼ�Σ����������ǽ�����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
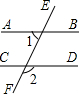 ��ͼ��ֱ��AB��CD��ֱ��EF���أ����AB��CD����1=55�㣬��ô��2=125�㣮
��ͼ��ֱ��AB��CD��ֱ��EF���أ����AB��CD����1=55�㣬��ô��2=125�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com