
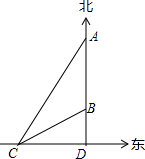
 如图,一艘巡洋舰从点A出发,沿正南方向航行了半小时到达点B,再沿南偏西60°方向航行了半小时到达点C,此时测得码头D在C的正东方向,该巡洋舰的速度为80海里/时.
如图,一艘巡洋舰从点A出发,沿正南方向航行了半小时到达点B,再沿南偏西60°方向航行了半小时到达点C,此时测得码头D在C的正东方向,该巡洋舰的速度为80海里/时.分析 (1)由路程=速度×时间得出AB=BC=80×$\frac{1}{2}$=40海里,解Rt△BCD,求出∠BCD=30°,根据30°角所对的直角边等于斜边的一半得出BD=$\frac{1}{2}$BC=20海里;
(2)由AB=BC,得出∠ACB=∠BAC,根据三角形外角的性质得出∠ACB+∠BAC=∠CBD=60°,那么∠BAC=∠ACB=30°,根据30°角所对的直角边等于斜边的一半得出CD=$\frac{1}{2}$AC.
解答 解:(1)由题意可得,AB=BC=80×$\frac{1}{2}$=40(海里),
在Rt△BCD中,∵∠BDC=90°,∠CBD=60°,
∴∠BCD=30°,
∴BD=$\frac{1}{2}$BC=20(海里),
即点B、D之间的距离为20海里;
(2)∵AB=BC,
∴∠ACB=∠BAC,
∵∠ACB+∠BAC=∠CBD=60°,
∴∠BAC=∠ACB=30°,
∴CD=$\frac{1}{2}$AC.
点评 本题考查了解直角三角形的应用-方向角问题,30°角所对的直角边等于斜边的一半的性质,等腰三角形的性质,三角形外角的性质,理解题意利用数形结合是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,已知C是线段AB上的一点,M,N分别是AC,BC的中点.
如图,已知C是线段AB上的一点,M,N分别是AC,BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
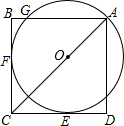 如图.圆心O在边长为2$\sqrt{2}$的正方形ABCD的对角线AC上,⊙O过点A,且BC,CD都相切,求$\widehat{AG}$的长.
如图.圆心O在边长为2$\sqrt{2}$的正方形ABCD的对角线AC上,⊙O过点A,且BC,CD都相切,求$\widehat{AG}$的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
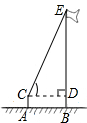 如图,小明在A点用测倾仪测得旗杆顶端E的仰角为69°,测倾仪的高度CA为1.55m,点A到旗杆底部B的距离为11.7m.求旗杆BE的高度(精确到1m)
如图,小明在A点用测倾仪测得旗杆顶端E的仰角为69°,测倾仪的高度CA为1.55m,点A到旗杆底部B的距离为11.7m.求旗杆BE的高度(精确到1m)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{1-a}$ | B. | $\frac{1}{a-1}$ | C. | -$\frac{2a-1}{a-1}$ | D. | $\frac{-2{a}^{2}-1}{a-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,河堤横断面迎水坡AB的破壁是$1:\sqrt{3}$,堤高BC=12cm,则坡面AB的长度是( )
如图,河堤横断面迎水坡AB的破壁是$1:\sqrt{3}$,堤高BC=12cm,则坡面AB的长度是( )| A. | 15cm | B. | $20\sqrt{3}$cm | C. | 24cm | D. | $10\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
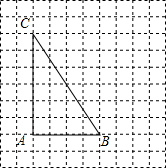 利用网格线画图:如图,点A、B、C都在正方形网格的格点上.
利用网格线画图:如图,点A、B、C都在正方形网格的格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com