
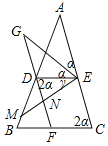
【题目】已知点D,E,F分别是△ABC的边AB,AC,BC上的点,DE∥BC,DF∥AC.
(1)如图1,点G是线段FD延长线上一点,连接EG,∠CEG的平分线EM交AB于点M,交FD于点N.则∠A,∠AME,∠CEG之间存在怎样的数量关系?请写出证明过程;
(2)如图2,在(1)的条件下,若EG平分∠AED,∠AME=35°,且∠EDF﹣∠A=30°,求∠C的度数.

【答案】(1)∠CEG=2∠A+2∠AME,证明详见解析;(2)68°.
【解析】
(1)利用外角定理即可求解;
(2)由平角AEC得:∠CEM+∠MED+∠DEA=180°,即:2α+γ+α+γ=180°;利用∠EDF﹣∠A=30°,得:2α﹣∠A=30°;利用∠CEM=∠AME=∠A,即可求解.
解:(1)∠CEM=∠A+∠AME,
而∠CEG=2∠CEM=2∠A+2∠AME;
(2)EG平分∠AED,设:∠GEA=∠GED=α,
DF∥AC,则∠EDF=2α,
由平角AEC得:∠CEM+∠MED+∠DEA=180°,
即:2α+γ+α+γ=180°…①,
∠EDF﹣∠A=30°,则2α﹣∠A=30°…②,
∠CEM=∠AME=∠A,
即:35°+∠A=α+γ…③,
联立①②③并解得:α=34°,
∠C=2α=68°.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】随着科技与经济的发展,中国廉价劳动力的优势开始逐渐消失,而作为新兴领域的机器人产业则迅速崛起,机器人自动化线的市场也越来越大,并且逐渐成为自动化生产线的主要方式,某化工厂要在规定时间内搬运1200千元化工原料.现有A,B两种机器人可供选择,已知A型机器人比B型机器人每小时多搬运30千克,A型机器人搬运900千克所用的时间与B型机器人搬运600千克所用的时间相等.


(1)两种机器人每小时分别搬运多少化工原料?
(2)该工厂原计划同时使用这两种机器人搬运,工作一段时间后,A型机器人又有了新的搬运任务,但必须保证这批化工原料在11小时内全部搬运完毕.求:A型机器人至少工作几个小时,才能保证这批化工原料在规定的时间内完成.
查看答案和解析>>
科目:初中数学 来源: 题型:
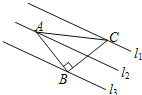
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
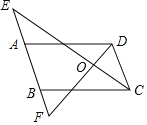
【题目】如图,已知∠DAE+∠CBF=180°,CE平分∠BCD,∠BCD=2∠E.
(1)求证:AD∥BC;
(2)CD与EF平行吗?写出证明过程;
(3)若DF平分∠ADC,求证:CE⊥DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两位同学在长方形的场地ABCD上绕着四周跑步,甲沿着A-D-C-B-A方向循环跑步,同时乙沿着B-C-D-A-B方向循环跑步,AB=30米,BC=50米,若甲速度为2米/秒,乙速度3米/秒.
(1)设经过的时间为t秒,则用含t的代数式表示甲的路程为 米;
(2)当甲、乙两人第一次相遇时,求所经过的时间t为多少秒?
(3)若甲改为沿着A-B-C-D-A的方向循环跑步,而乙仍按原来的方向跑步,两人的速度不变,求经过多少秒,乙追上甲?
(4)在(3)的条件下,当乙第一次追上甲后继续跑步,则最少再经过![]() 秒乙又追上甲,这时两人所处的位置在点P;直接写出
秒乙又追上甲,这时两人所处的位置在点P;直接写出![]() 的值,在图中标出点P,不要求书写过程.
的值,在图中标出点P,不要求书写过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
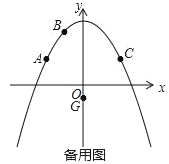
【题目】二次函数y=ax2+c的图象经过点A(﹣4,3),B(﹣2,6),点A关于抛物线对称轴的对称点为点C,点P是抛物线对称轴右侧图象上的一点,点G(0,﹣1).
(1)求出点C坐标及抛物线的解析式;
(2)若以A,C,P,G为顶点的四边形面积等于30时,求点P的坐标;
(3)若Q为线段AC上一动点,过点Q平行于y轴的直线与过点G平行于x轴的直线交于点M,将△QGM沿QG翻折得到△QGN,当点N在坐标轴上时,求Q点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:
宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.


第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,
第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,
问题解决:
(1)图③中AB=________(保留根号);
(2)如图③,判断四边形 BADQ的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
(4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
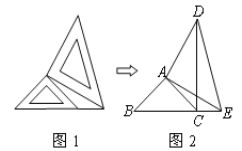
【题目】两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,图中AB=AC,AD=AE,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连结DC.
(1)图2中的全等三角形是_______________,并给予证明(说明:结论中不得含有未标识的字母);
(2)指出线段DC和线段BE的关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com