
 如图,在矩形纸片ABCD中,AB=8,AD=4,把矩形沿直线AC折叠,点B落在E处,连接DE,其中AE交DC于P.有下面四种说法:①AP=5;②△APC是等边三角形;③△APD≌△CPE;④四边形ACED为等腰梯形,且它的面积为25.6.其中正确的有个.
如图,在矩形纸片ABCD中,AB=8,AD=4,把矩形沿直线AC折叠,点B落在E处,连接DE,其中AE交DC于P.有下面四种说法:①AP=5;②△APC是等边三角形;③△APD≌△CPE;④四边形ACED为等腰梯形,且它的面积为25.6.其中正确的有个.
 ,
,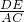 =
=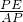 ,
, ,
, ×
× ×(
×( +
+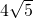 ),
),

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
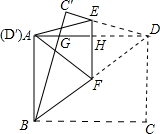 (2013•成都一模)如图,在矩形纸片ABCD中,AB=3,BC=4,把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合,则EF=
(2013•成都一模)如图,在矩形纸片ABCD中,AB=3,BC=4,把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合,则EF=| 25 |
| 12 |
| 25 |
| 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
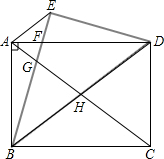 (2013•黄石模拟)如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F;
(2013•黄石模拟)如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F;查看答案和解析>>
科目:初中数学 来源: 题型:
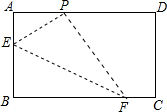 如图,在矩形纸片ABCD中,AB=8,BC=10.E、F为AB、BC边上两个动点,以EF为折痕折叠纸片,使点B恰好落在AD边上的点P处.当E、F运动时,点P也在一定范围内移动,则这个移动范围的最大距离为
如图,在矩形纸片ABCD中,AB=8,BC=10.E、F为AB、BC边上两个动点,以EF为折痕折叠纸片,使点B恰好落在AD边上的点P处.当E、F运动时,点P也在一定范围内移动,则这个移动范围的最大距离为查看答案和解析>>
科目:初中数学 来源: 题型:
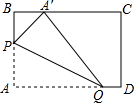 动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.
动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com