
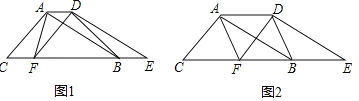
����Ŀ����ͼ������ȫ�ȵġ�ABC�͡�DEF�ص���һ�𣬹̶���ABC������DEF�������±任��
��1����ͼ1����DEF��ֱ��CB����ƽ�ƣ�����F���߶�CB���ƶ���������AF��AD��BD����ֱ��д��S��ABC��S�ı���AFBD�Ĺ�ϵ
��2����ͼ2������Fƽ�Ƶ��߶�BC���е�ʱ�����ı���AFBDΪ�����Σ���ô��ABCӦ����ʲô�����������֤����
��3���ڣ�2���������£�����DEF��DF�۵�����E����FA���ӳ����ϵĵ�G��������CG�����㻭��ͼ�Σ���ʱCG��CF�к�������ϵ��
���𰸡���1��S��ABC=S�ı���AFBD����2���ı���AFBDΪ�����Σ���3��CG=![]() CF��
CF��
��������
�����������1������ƽ���ߵ������Լ������������ϵ���ó��𰸣�
��2������ƽ���ı��ε��ж��ó��ı���AFBDΪƽ���ı��Σ������ó�AF=![]() BC=BF������𰸣�
BC=BF������𰸣�
��3���������⻭��ͼ�Σ���CF=k�����ù��ɶ���������ɣ�
�⣺��1��S��ABC=S�ı���AFBD��
���ɣ�������ɵã�AD��EC��
��S��ADF=S��ABD��
��S��ACF=S��ADF=S��ABD��
��S��ABC=S�ı���AFBD��
��2����ABCΪ����ֱ�������Σ�����AB=AC����BAC=90�㣬
�������£�
��FΪBC���е㣬
��CF=BF��
��CF=AD��
��AD=BF��
�֡�AD��BF��
���ı���AFBDΪƽ���ı��Σ�
��AB=AC��FΪBC���е㣬
��AF��BC��
��ƽ���ı���AFBDΪ����
�ߡ�BAC=90�㣬FΪBC���е㣬
��AF=![]() BC=BF��
BC=BF��
���ı���AFBDΪ�����Σ�
��3����ͼ3��ʾ��

�ɣ�2��֪����ABCΪ����ֱ�������Σ�AF��BC��
��CF=k����GF=EF=CB=2k��
�ɹ��ɶ����ã�CG=![]() k��
k��
��CG=![]() CF��
CF��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��1.58��106�İ����֮һ��Լ�ǣ� ��
A������ѧ��С�������� B�����Һڰ�ij���
C�������п����Ŀ��� D������¥���ĸ߶�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȥ��ʮһ�ƽ����ڼ䣬��Ȫ��7����ÿ�����������ı仯������±���������ʾ��9��30�ն��������������ʾ��9��30���ٵ���������
���� | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� | 7�� |
�����仯/���� | +0.5 | +0.7 | +0.8 |
|
| +0.2 |
|
(1)�����ж�7�����ο��������������ٵĸ�����һ�죿�������������ˣ�
(2)�����9��30����������Ϊ2���ˣ�ƽ��ÿ������300Ԫ�����ʷ羰���ڴ�7����������Ϊ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ����
a�����ĸ�������-1 ��b������ֵ���ڱ���������������c����������Ϊ���������������������㣻d�������ϱ�ʾ-a�ĵ�һ����ԭ����ߣ�e����������7��9֮�����������8.
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ÿ��50ǧ��Ϊ���������ļ�Ϊ��������ļ�Ϊ����������¼���£�+4.5����4��+2.3����3.5��+2.5������������������� _____________ǧ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���У� ��
������������ֻ��һ��ֱ�ߣ�
������������߶ν�������ľ��룻
������֮�䣬�߶���̣�
����AB��BC�����B���߶�AC���е㣻
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1������6��+��+8������+4��������2��
��2������7��������5����90�£���15��
��3����![]() ��
��![]() +
+![]() ��������36��
��������36��
��4��2�£���![]() ����
����![]() �£���
�£���![]() ��
��
��5����24+��4��9��2��5������1��6
��6���ü�㷽�����㣺����370��������![]() ��+0.25��24.5��5
��+0.25��24.5��5![]() ������25%��
������25%��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��
(1)(3a2��ab��7)��(5ab��4a2��7)������ a��2��b��![]() ��
��
(2)3(ab��5b2��2a2)��(7ab��16a2��25b2)������|a��1|��(b��1)2��0.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com