
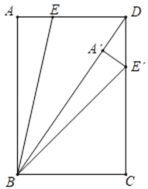
【题目】如图,在矩形ABCD中,AB=8,BC=6,E为AD上一点,将△BAE绕点B顺时针旋转得到△BA′E′,当点A′,E′分别落在BD,CD上时,则DE的长为_____.
科目:初中数学 来源: 题型:
【题目】定义:我们把关于某一点成中心对称的两条抛物线叫“孪生抛物线”;(1)已知抛物线L:y=﹣x2+4与x轴交于A、B两点(A在B的左侧),与y轴交于C点,求L关于坐标原点O(0,0)的“孪生抛物线”W;(2)点N为坐标平面内一点,且△BCN是以BC为斜边的等腰直角三角形,在x轴是否存在一点M(m,0),使抛物线L关于点M的“孪生抛物线”过点N,如果存在,求出M点坐标;不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
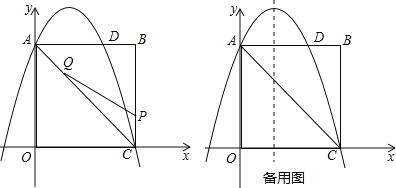
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在参加了成都市教育质量综合评价学业素养测试后,随机抽取八年级部分学生,针对发展水平四个维度:A﹣阅读素养、B﹣数学素养、C﹣科学素养、D﹣人文素养,开展了“你最需要提升的学业素养”问卷调查(每名学生必选且只能选择一项).现将调查的结果绘制成如图两幅不完整的统计图.
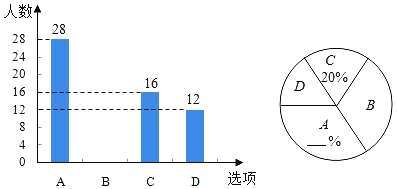
(1)求本次调查的学生总人数,并补全两幅统计图;
(2)求扇形统计图中的选项D对应的扇形圆心角的度数;
(3)该校八年级共有学生400人,请估计全年级选择选项B的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
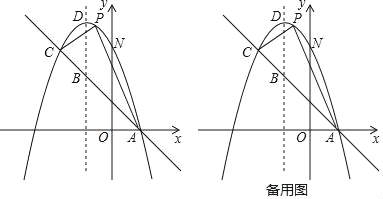
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴分别交于
与x轴分别交于![]() ,
,![]() 两点,与y轴交于点C.
两点,与y轴交于点C.
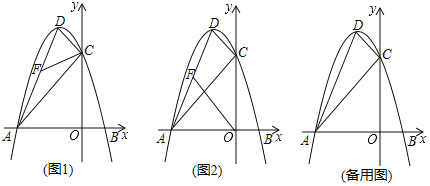
(1)求抛物线的表达式及顶点D的坐标;
(2)点F是线段AD上一个动点.
①如图1,设![]() ,当k为何值时,
,当k为何值时,![]() .
.
②如图2,以A,F,O为顶点的三角形是否与![]() 相似?若相似,求出点F的坐标;若不相似,请说明理由.
相似?若相似,求出点F的坐标;若不相似,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com