

���� ��1�������������C�����꣬����á�OCP�������
��2���ɶԳƵ����ʿ�֪��OPC�ա�OP��C����֪OD��AB�����������ȿ����OD���������OP�������C�����ꣻ
��3������C��t��-$\frac{3}{4}$t+3���������Ե�CΪ����������ߣ���ù���t�ĸ������ɹ���D��DE��CP�ڵ�E�����DEC=��AOB=90�㣬���ɡ�DEC�ס�AOB�Ӷ����CD��
�������������COD�����Ϊ��ֵ������Rt��PCO��Rt��OAB�����߶α�����tΪ$\frac{36}{25}$ʱ��h���
��� �⣺��1����PC��x�ᣬ
�൱OP=1ʱ����C��ĺ�����Ϊ1��
��C��ֱ��AB�ϣ���x=1ʱ����������y=$\frac{9}{4}$����PC=$\frac{9}{4}$��
��S��OCP=$\frac{1}{2}$OP•PC=$\frac{1}{2}$��1��$\frac{9}{4}$=$\frac{9}{8}$��
�ʴ�Ϊ��$\frac{9}{8}$��
��2������P����ֱ��OC�ĶԳƵ�P������ֱ��AB��ʱ����ͼ1��
�ڡ�OPC�͡�OP��C�У�
$\left\{\begin{array}{l}{OP=OP��}\\{PC=P��C}\\{OC=OC}\end{array}\right.$��
���OPC�ա�OP��C��SSS����
��OP=OP�䣬�ҡ�OP��C=��OPC=90�㣬
��Rt��OAB��OA=4��OB=3�������AB=5��
��OP��=$\frac{OA•OB}{AB}$=$\frac{12}{5}$��
��OP=$\frac{12}{5}$����C�������Ϊx=$\frac{12}{5}$������ֱ��AB����ʽ�����y=$\frac{6}{5}$��
��C��������$\frac{12}{5}$��$\frac{6}{5}$����
��3����������ã�C��t��-$\frac{3}{4}$t+3����
����CΪ����������߽���ʽ��y=��x-t��2-$\frac{3}{4}$t+3��
�ɣ�x-t��2-$\frac{3}{4}$t+3=-$\frac{3}{4}$x+3��
����x-t��2+$\frac{3}{4}$��x-t��=0��
�ࣨx-t����x-t+$\frac{3}{4}$��=0��
���x1=t��x2=t-$\frac{3}{4}$��
����D��DE��CP�ڵ�E����ͼ2�����DEC=��AOB=90�㣬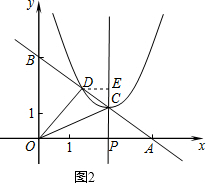
��DE��OA��
���EDC=��OAB��
���DEC�ס�AOB��
��$\frac{DE}{AO}$=$\frac{CD}{BA}$��
��AO=4��AB=5��DE=t-��t-$\frac{3}{4}$��=$\frac{3}{4}$��
��CD=$\frac{DE•BA}{AO}$=$\frac{\frac{3}{4}��5}{4}$=$\frac{15}{16}$��
�ڡ�CD=$\frac{15}{16}$��CD���ϵĸ�=$\frac{3��4}{5}$=$\frac{12}{5}$��
��S��COD=$\frac{1}{2}$��$\frac{15}{16}$��$\frac{12}{5}$=$\frac{9}{8}$��
��S��CODΪ��ֵ��
ҪʹOC���ϵĸ�h��ֵ���ֻҪOC��̣���Ϊ��OC��ABʱOC��̣���ʱOC�ij�Ϊ$\frac{12}{5}$����BCO=90�㣬
�ߡ�AOB=90�㣬
���COP=90��-��BOC=��OBA��
�֡�CP��OA��
��Rt��PCO��Rt��OAB��
��$\frac{OP}{BO}$=$\frac{OC}{BA}$��
��OP=$\frac{OC•BO}{BA}$=$\frac{\frac{12}{5}��3}{5}$=$\frac{36}{25}$��
����OPΪ$\frac{36}{25}$ʱ��h��ֵ���
���� ������Ҫ������κ������ۺ�Ӧ�ã��漰�����ε��������������뺯������ʽ�Ĺ�ϵ�����κ�������ʽ��������ȫ�ȡ����Ƶ��ж������ʵ�֪ʶ�㣮�ڣ�1�������õ�������뺯������ʽ�Ĺ�ϵ���CP�ǽ���Ĺؼ����ڣ�2���еó�OP���AB�ǽ���Ĺؼ����ڣ�3��������t��ʾ��DE���������������ε��������CD���ڢ����жϳ���OCD���������ǽ���Ĺؼ��������漰֪ʶ��϶࣬�ۺ��Խ�ǿ���ѶȺܴ�


 �߽�������ϵ�д�
�߽�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
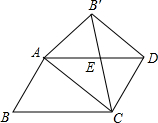 ����֪��ƽ���ı����кܶ����ʣ�����������ǰ�ƽ���ı�����������һ���Խ��߷��ۣ��ᷢ�������л��и���Ľ��ۣ�
����֪��ƽ���ı����кܶ����ʣ�����������ǰ�ƽ���ı�����������һ���Խ��߷��ۣ��ᷢ�������л��и���Ľ��ۣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ��l��m���ȱߡ�ABC�Ķ���B��ֱ��m�ϣ���BC��ֱ��m�������Ϊ25�㣬��Ϧ��Ķ���Ϊ35�㣮
��֪����ͼ��l��m���ȱߡ�ABC�Ķ���B��ֱ��m�ϣ���BC��ֱ��m�������Ϊ25�㣬��Ϧ��Ķ���Ϊ35�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
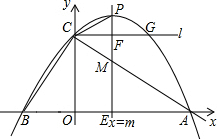 ��ͼ��ֱ��y=2x+4��x�ᡢy���ཻ��B��C���㣬������y=ax2-3ax+c����B��C������x����һ������ΪA������C��x���ƽ����l�����������ڵ�G��
��ͼ��ֱ��y=2x+4��x�ᡢy���ཻ��B��C���㣬������y=ax2-3ax+c����B��C������x����һ������ΪA������C��x���ƽ����l�����������ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x+3��2=8 | B�� | ��x-3��2=1 | C�� | ��x-3��2=10 | D�� | ��x+3��2=4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����Խ����Ƿ��ƽ�� | B�� | ��������Ա��Ƿ�ֱ���� | ||
| C�� | �����Խ����Ƿ���� | D�� | ���������������Ƿ�Ϊֱ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m=-1��n=5 | B�� | m=1��n=5 | C�� | m=-1��n=-5 | D�� | m=1��n=-5 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com