
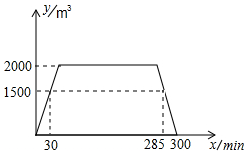
 某游泳池一天要经过“注水-保持-排水”三个过程,如图,图中折线表示的是游泳池在一天某一时间段内池中水量y(m3)与时间x(min)之间的关系.
某游泳池一天要经过“注水-保持-排水”三个过程,如图,图中折线表示的是游泳池在一天某一时间段内池中水量y(m3)与时间x(min)之间的关系.分析 (1)根据函数图象中的数据可以求得排水阶段y与x之间的函数关系式,并写出x的取值范围;
(2)根据图象可以求出注水阶段的函数解析式,从而可以求得水量不超过最大水量的一半值的时间一共有多少分钟.
解答 解:(1)设排水阶段y与x之间的函数关系式是y=kx+b,
$\left\{\begin{array}{l}{285k+b=1500}\\{300k+b=0}\end{array}\right.$,得$\left\{\begin{array}{l}{k=-100}\\{b=30000}\end{array}\right.$,
即排水阶段y与x之间的函数关系式是y-100x+30000,
当y=2000时,2000=-100x+30000,得x=280,
即排水阶段y与x之间的函数关系式y=-100x+30000(280≤x≤300);
(2)设注水阶段y与x的函数关系式为y=mx,
则30m=1500,得m=50,
∴注水阶段y与x的函数关系式为:y=50x,
当y=1000时,1000=50x,得x=20,
将y=1000代入y=-100x+30000,得x=290,
∴水量不超过最大水量的一半值的时间一共有:20+(300-290)=30(分钟),
即水量不超过最大水量的一半值的时间一共有30分钟.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质解答.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,E是△ABC中BC边上的一点,且BE=$\frac{1}{3}$BC;点D是AC上一点,且AD=$\frac{1}{4}$AC,S△ABC=24,则S△BEF-S△ADF=( )
如图,E是△ABC中BC边上的一点,且BE=$\frac{1}{3}$BC;点D是AC上一点,且AD=$\frac{1}{4}$AC,S△ABC=24,则S△BEF-S△ADF=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
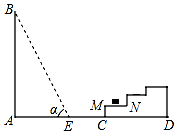 如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=34.5米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=20米,现有一只小猫睡在台阶的MN这层上晒太阳.($\sqrt{3}$取1.73)
如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=34.5米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=20米,现有一只小猫睡在台阶的MN这层上晒太阳.($\sqrt{3}$取1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABC中,∠C=90°,AC=8,BC=6.
如图,Rt△ABC中,∠C=90°,AC=8,BC=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com