
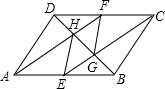
 如图,已知在平行四边形ABCD中,点E、F分别是AB、CD的中点,CE、AF与对角线BD分别相交于点G、H,联结EH、FG.
如图,已知在平行四边形ABCD中,点E、F分别是AB、CD的中点,CE、AF与对角线BD分别相交于点G、H,联结EH、FG.分析 (1)连接EF,交BD于点O,根据对角线互相平分的四边形是平行四边形即可证明四边形EGFH是平行四边形;
(2)根据对角线互相垂直的平行四边形是菱形即可求证.
解答  (1)解:连接EF,交BD于点O.
(1)解:连接EF,交BD于点O.
∵AB∥CD,AB=CD,点E、F分别是AB、CD的中点,
∴$\frac{FO}{EO}$=$\frac{OD}{BO}$=$\frac{DF}{BE}$=$\frac{\frac{1}{2}CD}{\frac{1}{2}AB}$=1.
∴FO=EO,DO=BO.
∵DH=GB,
∴OH=OG.
∴四边形EGFH是平行四边形.
(2)证明:由(1)知,四边形EGFH是平行四边形.
∵点E、O分别是AB、BD的中点,
∴OE∥AD.
∵AD⊥BD,
∴EF⊥GH.
∴?HEGF是菱形.
点评 本题主要考查了平行线分线段成比例定理,以及菱形的判定,正确理解定理是解决本题的关键.


科目:初中数学 来源: 题型:解答题
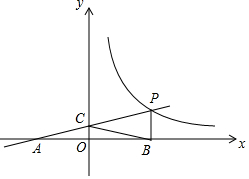 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
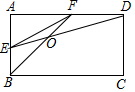 如图,在矩形ABCD中,E、F分别是AB、AD的中点,连接BF、DE交于点O,连接EF,给出如下结论:
如图,在矩形ABCD中,E、F分别是AB、AD的中点,连接BF、DE交于点O,连接EF,给出如下结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
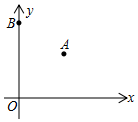 平面直角坐标系中,A(3,3)、B(0,5).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
平面直角坐标系中,A(3,3)、B(0,5).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )| A. | 3 | B. | 4 | C. | 5 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.如果第一次随机摸出一个小球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)
在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.如果第一次随机摸出一个小球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com