
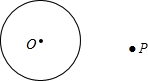
 我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)
我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论) 科目:初中数学 来源: 题型:填空题
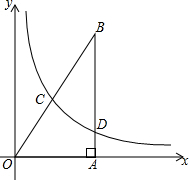 如图,Rt△ABC中,∠OAB=90°,直角边OA在平面直角坐标系的x轴上,O为坐标原点,OA=2,AB=4,函数y=$\frac{k}{x}$(x>0)的图象分别与BO、BA交于C、D两点,且以B、C、D为顶点的三角形与△OAB相似,则k的值为$\frac{1}{2}$.
如图,Rt△ABC中,∠OAB=90°,直角边OA在平面直角坐标系的x轴上,O为坐标原点,OA=2,AB=4,函数y=$\frac{k}{x}$(x>0)的图象分别与BO、BA交于C、D两点,且以B、C、D为顶点的三角形与△OAB相似,则k的值为$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
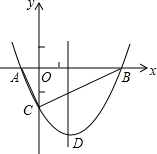 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,已知AB=4,AC=3,BC=5,以BC所在的直线为y轴,以点C为原点建立平面直角坐标系.x轴交AD于点E,有一动点P以5个单位/秒的速度熊A点出发,到达B点,再到C点停止,另一动点F以3个单位/秒的速度从C点出发向x轴的正方向运动,和点P同时开始,同时停止运动,令运动的时间为t.
如图,在平行四边形ABCD中,已知AB=4,AC=3,BC=5,以BC所在的直线为y轴,以点C为原点建立平面直角坐标系.x轴交AD于点E,有一动点P以5个单位/秒的速度熊A点出发,到达B点,再到C点停止,另一动点F以3个单位/秒的速度从C点出发向x轴的正方向运动,和点P同时开始,同时停止运动,令运动的时间为t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
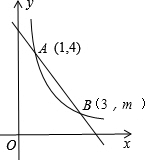 如图,在直角坐标系xOy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(1,4),B(3,m)两点.
如图,在直角坐标系xOy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(1,4),B(3,m)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
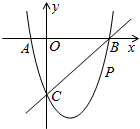 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点左侧,B点的坐标为(4,0),与y轴交于C(0,-4)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点左侧,B点的坐标为(4,0),与y轴交于C(0,-4)点,点P是直线BC下方的抛物线上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
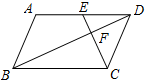 如图,平行四边形ABCD中,点E是AD边上一点,且 CE⊥BD于点F,将△DEC沿从D到A的方向平移,使点D与点A重合,点E平移后的点记为G.
如图,平行四边形ABCD中,点E是AD边上一点,且 CE⊥BD于点F,将△DEC沿从D到A的方向平移,使点D与点A重合,点E平移后的点记为G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
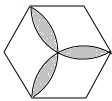 向如图所示的正六边形靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
向如图所示的正六边形靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )| A. | $\frac{2\sqrt{3}-π}{π}$ | B. | $\frac{2π\sqrt{3}-9}{9}$ | C. | $\frac{π-\sqrt{3}}{π}$ | D. | $\frac{π\sqrt{3}-4}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com