
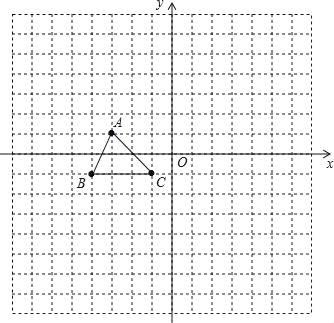
【题目】如图,点A、B、C的坐标分别为(﹣3,1)、(﹣4,﹣1)、(﹣1,﹣1),将△ABC先向下平移2个单位,得△A1B1C1;再将△A1B1C1沿y轴翻折180°,得△A2B2C2;.
(1)画出△A1B1C1和△A2B2C2;
(2)求直线A2A的解析式.
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,点
,点![]() 是线段
是线段![]() 的中点,先按要求画图形,再解决问题.
的中点,先按要求画图形,再解决问题.
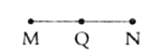
(1)延长线段![]() 至点
至点![]() ,使
,使![]() ;延长线段
;延长线段![]() 至点
至点![]() ,使
,使![]() ;(尺规作图,保留作图痕迹)
;(尺规作图,保留作图痕迹)
(2)求线段![]() 的长度;
的长度;
(3)若点![]() 是线段
是线段![]() 的中点,求线段
的中点,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
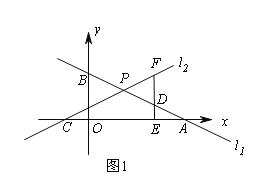
【题目】平面直角坐标系中,直线l1:![]() 与x轴交于点A,与y轴交于点B,直线l2:
与x轴交于点A,与y轴交于点B,直线l2:![]() 与x轴交于点C,与直线l1交于点P.
与x轴交于点C,与直线l1交于点P.
(1)当k=1时,求点P的坐标;
(2)如图1,点D为PA的中点,过点D作DE⊥x轴于E,交直线l2于点F,若DF=2DE,求k的值;
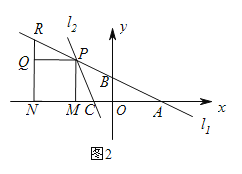
(3)如图2,点P在第二象限内,PM⊥x轴于M,以PM为边向左作正方形PMNQ,NQ的延长线交直线l1于点R,若PR=PC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
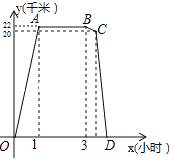
【题目】某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.
(1)活动中心与小宇家相距 千米,小宇在活动中心活动时间为 小时,他从活动中心返家时,步行用了 小时;
(2)求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);
(3)根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 | 面试 | 笔试 | ||
形体 | 口才 | 专业水平 | 创新能力 | |
甲 | 86 | 90 | 96 | 92 |
乙 | 92 | 88 | 95 | 93 |
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照4:6:5:5的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.
(1)求证:△PFA∽△ABE;
(2)当点P在线段AD上运动时,设PA=x,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由;
(3)探究:当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,请直接写出x满足的条件: .

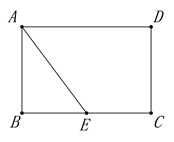
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
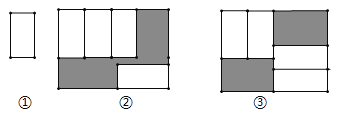
【题目】把四张大小相同的长方形卡片(如图①)按图②、图③两种放法放在一个底面为长方形(长为![]() ,宽为
,宽为![]() )的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为
)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为![]() ,图③中阴影部分的周长为
,图③中阴影部分的周长为![]() ,则
,则![]() ___________.
___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com