
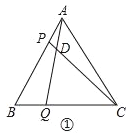
【题目】边长为6的等边△ABC中,点P从点A出发沿射线AB方向移动,同时点Q从点B出发,以相同的速度沿射线BC方向移动,连接AQ、CP,直线AQ、CP相交于点D.
(1)如图①,当点P、Q分别在边AB、BC上时,
①连接PQ,当△BPQ是直角三角形时,AP等于_____;
②∠CDQ的大小是否随P,Q的运动而变化?如果不会,请求出∠CDQ的度数;如果会,请说明理由;
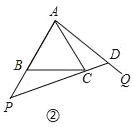
(2)当P、Q分别在边AB、BC的延长线上时,在图②中画出点D,并直接写出∠CDQ的度数.
【答案】(1)①2或4;②60°;(2)120°.
【解析】分析:
(1)①如图3,由题意可知∠B=60°,然后分∠PQB=90°和∠QPB=90°两种情况结合已知条件进行解答即可;②由已知条件易证△ABQ≌△CAP,由此可得∠BAQ=∠ACP,从而可得∠CDQ=∠DAC+∠ACP=∠DAC+∠BAQ=∠CAB=60°,由此可得∠CDQ的大小不随点P、Q的运动而改变;
(2)如图4,由题意易证△ABQ≌△CAP,从而可得∠Q=∠P,结合∠P+∠BCP=60°可得∠Q+∠DCQ=60°,从而可得此时∠CDQ=120°.
详解:
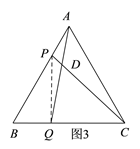
(1)如图3,连接PQ,
①∵△ABC是等边三角形,
∴∠B=60°,
由题意得,AP=BQ,
当∠PQB=90°时,BQ=![]() BP,即AP=
BP,即AP=![]() (6﹣AP)
(6﹣AP)
解得,AP=2,
当∠QPB=90°时,BQ=2BP,即AP=2(6﹣AP)
解得,AP=4,
综上所述,当AP=2或4时,△BPQ是直角三角形,
故答案为:2或4;
②∠CDQ的大小不变
∵P、Q用时出发,速度相同,所以AP=BQ,
∵△ABC是等边三角形,
∴BA=AC,∠B=∠CAP=60°,
在△ABQ和△CAP中,
BA=AC,∠B=∠APC,BQ=AP,
∴△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∴∠CDQ=∠DAC+∠ACP=∠DAC+∠BAQ=∠CAB=60°;
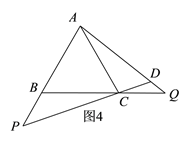
(2)如图4,∠CDQ=120°,理由如下:
∵△ABC是等边三角形,
∴BA=AC,∠ABC=∠CAP=60°,
在△ABQ和△CAP中,
BA=AC,∠ABQ=∠CAP,BQ=AP,
∴△ABQ≌△CAP,
∴∠Q=∠P,
∵∠P+∠BCP=60°,
∴∠Q+∠DCQ=60°,
∴∠CDQ=120°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:我国数学家华罗庚在一次出国访问途中,看到飞机上:邻座的乘客阅读的杂志上有一道智力题,求59319的立方根,华罗庚脱口而击.众人惊命,忙问计算奥妙.你知道怎样迅速准确地计算出结果的吗?诺按照下面的分析试一试
(1)由103=1000,1003=100000,可知![]() 是 位数;
是 位数;
(2)由59319的个位数是9,可知![]() 的个位数是 ;
的个位数是 ;
(3)如果划去59319后面的三位319得到59,而33=27,43=64,由此确定![]() 的十位数是 .
的十位数是 .
请应用以上方法计算:![]() = .
= . ![]() =
=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面积为
;④△ABF的面积为![]() .其中一定成立的有几个( )
.其中一定成立的有几个( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初中各年级学生每天的平均睡眠时间(单位:h,精确到1 h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
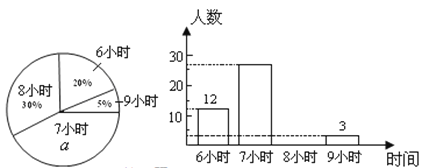
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数![]() 的值为_______,所抽查的学生人数为______;
的值为_______,所抽查的学生人数为______;
(2)求出平均睡眠时间为8小时的人数,并补全条形图;
(3)求出这部分学生的平均睡眠时间的平均数;
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
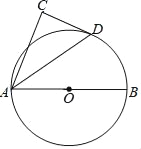
【题目】如图,AB为⊙O的直径,D为⊙O上一点,以AD为斜边作△ADC,使∠C=90°,∠CAD=∠DAB
(1)求证:DC是⊙O的切线;
(2)若AB=9,AD=6,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个边长分别为a、b(![]() >
>![]() )的正方形纸片叠放在一起.(用含有a、b的代数式表示问题的结果)
)的正方形纸片叠放在一起.(用含有a、b的代数式表示问题的结果)
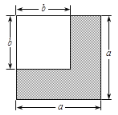
⑴请用至少两种方法求出图中阴影部分的面积;
⑵ 由面积相等,你发现了怎样的等量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节吃粽子是中华民族的传统习惯.农历五月初五早晨,小王的妈妈用不透明袋子装着一些粽子(粽子除食材不同外,其他一切相同),其中糯米粽两个,还有一些薯粉粽,现小王从中任意拿出一个是糯米粽的概率为![]() .
.
(1)求袋子中薯粉粽的个数;
(2)小王第一次任意拿出一个粽子(不放回),第二次再拿出一个粽子,请你用树形图或列表法,求小王两次拿到的都是薯粉粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
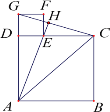
【题目】如图,已知四边形![]() 和四边形
和四边形![]() 为正方形,点
为正方形,点![]() 在线段
在线段![]() 上,点
上,点![]() 在同一直线上,连接
在同一直线上,连接![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
(3)设![]() ,
,![]() ,当点H是线段GC的中点时,则
,当点H是线段GC的中点时,则![]() 与
与![]() 满足什么样的关系式.
满足什么样的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com