
请阅读下面材料:
若 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.
为此抛物线的对称轴.
有一种方法证明如下:
|
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点, ∴
(a ≠ 0)上不同的两点, ∴ 且
且  ≠
≠ .
.  .
. .
. .
. (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为 ,
, 为此抛物线的对称轴.
为此抛物线的对称轴.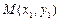 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,直线
(a ≠ 0)上不同的两点,直线 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取 ,
, 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程; 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.  智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:阅读理解
| x1+x2 |
| 2 |
|
| b |
| a |
| b |
| 2a |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| x1+x2 |
| 2 |
|
| b |
| a |
| b |
| 2a |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.
为此抛物线的对称轴.
|
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点, ∴
(a ≠ 0)上不同的两点, ∴ 且
且  ≠
≠ .
.  .
. .
. .
. (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为 ,
, 为此抛物线的对称轴.
为此抛物线的对称轴.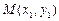 ,
,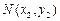 是抛物线
是抛物线 (a ≠ 0)上不同的两点,直线
(a ≠ 0)上不同的两点,直线 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取 ,
, 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程; 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.查看答案和解析>>
科目:初中数学 来源:2010-2011学年江苏省南通市如东县九年级(上)期末数学试卷(解析版) 题型:解答题
 为此抛物线的对称轴.
为此抛物线的对称轴. 且 x1≠x2.
且 x1≠x2.
 ,
, 为此抛物线的对称轴.
为此抛物线的对称轴. 为该抛物线的对称轴,那么自变量取x1,x2时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
为该抛物线的对称轴,那么自变量取x1,x2时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com