
分析 (1)原式利用立方差公式分解即可;
(2)原式提取公因式,再利用立方差公式分解即可;
(3)原式提取公因式,再利用立方差公式分解即可;
(4)原式提取公因式,再利用立方和公式分解即可.
解答 解:(1)原式=(2-m)(4+2m+m2);
(2)原式=$\frac{1}{8}$(m3-$\frac{1}{8}$n3)=$\frac{1}{8}$(m-$\frac{1}{2}$n)(m2+$\frac{1}{2}$mn+$\frac{1}{4}$n2);
(3)原式=(2xy-5)(4x2y2+10xy+25);
(4)原式=(2x+3y)(4x2-6xy+9y2).
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:选择题
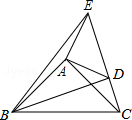 如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2<2(AD2+AB2).其中结论正确的个数是( )
如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2<2(AD2+AB2).其中结论正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
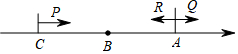 如图,已知数轴上有三点A、B、C,AC=2AB,AB=60,点A对应的数是40.动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少4个单位长度/秒,经过5秒,点P、R之间的距离与点Q、R之间的距离相等,动点Q的速度为4或20个单位长度/秒.
如图,已知数轴上有三点A、B、C,AC=2AB,AB=60,点A对应的数是40.动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少4个单位长度/秒,经过5秒,点P、R之间的距离与点Q、R之间的距离相等,动点Q的速度为4或20个单位长度/秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
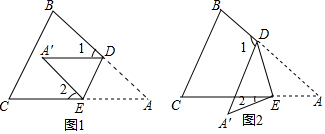
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
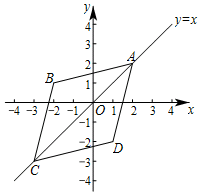 在平面直角坐标系xOy中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y=x上,那么称该菱形为点A,C的“极好菱形”.如图为点A,C的“极好菱形”的一个示意图.
在平面直角坐标系xOy中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y=x上,那么称该菱形为点A,C的“极好菱形”.如图为点A,C的“极好菱形”的一个示意图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com