
【题目】下面是小明主设计的“作一个含30°角的直角三角形”的尺规作图过程.
已知:直线l.
![]()
求作:△ABC,使得∠ACB=90°,∠ABC=30°.
作法:如图,
![]()
①在直线l上任取两点O,A;
②以点O为圆心,OA长为半径画弧,交直线l于点B;
③以点A为圆心,AO长为半径画弧,交![]() 于点C;
于点C;
④连接AC,BC.
所以△ABC就是所求作的三角形.
根据小明设计的尺规作图过程:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:在⊙O中,AB为直径,
∴∠ACB=90°(① ),(填推理的依据)
连接OC
∵OA=OC=AC,
∴∠CAB=60°,
∴∠ABC=30°(② ),(填推理的依据)
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线l经过B、C两点,点M从点A出发以每秒1个单位长度的速度向终点B运动,连接CM,将线段MC绕点M顺时针旋转90°得到线段MD,连接CD、BD.设点M运动的时间为t(t>0),请解答下列问题:
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线l经过B、C两点,点M从点A出发以每秒1个单位长度的速度向终点B运动,连接CM,将线段MC绕点M顺时针旋转90°得到线段MD,连接CD、BD.设点M运动的时间为t(t>0),请解答下列问题:

(1)求点A的坐标与直线l的表达式;
(2)①请直接写出点D的坐标(用含t的式子表示),并求点D落在直线l上时t的值;
②求点M运动的过程中线段CD长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
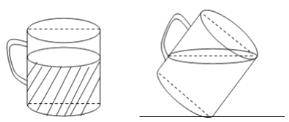
【题目】如图,有一个底面直径与杯高均为![]() 的杯子里面盛了一些溶液,当它支在桌子上倾斜到液面与杯壁呈
的杯子里面盛了一些溶液,当它支在桌子上倾斜到液面与杯壁呈![]() 才能将液体倒出,则此时杯子最高处距离桌面________
才能将液体倒出,则此时杯子最高处距离桌面________![]() .(
.(![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的例题及点拨,并解决问题:
例题:如图①,在等边△ABC中,M是BC边上一点(不含端点B,C),N是△ABC的外角∠ACH的平分线上一点,且AM=MN.求证:∠AMN=60°.
点拨:如图②,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连接EM.易证:△ABM≌△EBM(SAS),可得AM=EM,∠1=∠2;又AM=MN,则EM=MN,可得∠3=∠4;由∠3+∠1=∠4+∠5=60°,进一步可得∠1=∠2=∠5,又因为∠2+∠6=120°,所以∠5+∠6=120°,即:∠AMN=60°.
问题:如图③,在正方形A1B1C1D1中,M1是B1C1边上一点(不含端点B1,C1),N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点,且A1M1=M1N1.求证:∠A1M1N1=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
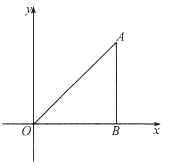
【题目】如图,将一个直角三角形纸片![]() ,放置在平面直角坐标系中,点
,放置在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() .将
.将![]() 沿
沿![]() 翻折得到
翻折得到![]() (点
(点![]() 为点
为点![]() 的对应点).
的对应点).
(Ⅰ)求![]() 的长及点
的长及点![]() 的坐标;
的坐标;
(Ⅱ)点![]() 是线段
是线段![]() 上的点,点
上的点,点![]() 是线段
是线段![]() 上的点.
上的点.
①已知![]() ,
,![]() ,
,![]() 是
是![]() 轴上的动点,当
轴上的动点,当![]() 取最小值时,求出点
取最小值时,求出点![]() 的坐标及点
的坐标及点![]() 到直线
到直线![]() 的距离;
的距离;
②连接![]() ,
,![]() ,且
,且![]() ,现将
,现将![]() 沿
沿![]() 翻折得到
翻折得到![]() (点
(点![]() 为点
为点![]() 的对应点),再将
的对应点),再将![]() 绕点
绕点![]() 顺时针旋转,旋转过程中,射线
顺时针旋转,旋转过程中,射线![]() ,
,![]() 交直线
交直线![]() 分别为点
分别为点![]() ,
,![]() ,最后将
,最后将![]() 沿
沿![]() 翻折得到
翻折得到![]() (点
(点![]() 为点
为点![]() 的对应点),连接
的对应点),连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在A、B两个校区各有九年级学生200人,为了解这两个校区九年级学生的教学学业水平的情况,进行了抽样调查,过程如下,请补充完整.
收集数据:从A、B两个校区各随机抽取20名学生,进行了数学学业水平测试,测试成绩(百分制)如下:
A校区 86 74 78 81 76 75 86 70 75 90
75 79 81 70 74 80 87 69 83 77
B校区 80 73 70 82 71 82 83 93 77 80
81 93 81 73 88 79 81 70 40 83
整理、描述数据 按如下分数段整理、描述这两组样本数据:
成绩x 人数 校区 | 40≤x<50 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
A | 0 | 0 | 1 | 11 | 7 | 1 |
B |
(说明:成绩80分及以上的学业水平优秀,70﹣79分为淡定业水平良好,60﹣69分为学业水平合格,60分以下为学业水平不合格)
分析数据 两组样本数据的平均数、中位数、众数如下表所示:
校区 | 平均数 | 中位数 | 众数 |
A | 78.3 | m | 75 |
B | 78 | 80.5 | 81 |
其中m= ;
得出结论:a.估计B校区九年级数学学业水平在优秀以上的学生人数为 ;
b.可以推断出 校区的九年级学生的数学学业水平较高,理由为 (至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”以其颠覆性的创新,赢得了数亿人的支持,为了调查某中学学生在周日上“微信”的时间,随机对100名男生和100名女生进行了问卷调查,得到了如下的统计结果
表1:男生上“微信时间的频数分布表
上网时间(分钟) | 30≤x<40 | 40≤x<50 | 50≤x<60 | 60≤x<70 | 70≤x<80 |
人数 | 5 | 25 | 30 | 25 | 15 |
表2:女生上“微信”时间的频数分布表
上网时间(分钟) | 30≤x<40 | 40≤x<50 | 50≤x<60 | 60≤x<70 | 70≤x<80 |
人数 | 10 | 20 | 40 | 20 | 10 |
请结合图表完成下列各题
(1)完成表3:
表3 | 上“微信”时间少于60分钟 | 上“微信”时间不少于60分钟 |
男生人数 |
|
|
女生人数 |
|
|
(2)若该中学共有女生750人,请估计其中上“微信”时间不少于60分钟的人数;
(3)从表3的男生中抽取5人(其中3人上“微信”时间少于60分钟,2人上“微信”时间不少于60分钟),再从抽取的5人中任取2人,请用列表或画树状图的方法求出至少有一人上“微信”时间不少于60分钟的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() 与
与![]() 轴交于点
轴交于点![]() 二次函数
二次函数![]() 的图象经过
的图象经过![]() 两点,且与
两点,且与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.

![]() 求二次函数的解析式及点
求二次函数的解析式及点![]() 的坐标.
的坐标.
![]() 点
点![]() 是线段
是线段![]() 上的一动点,动点
上的一动点,动点![]() 在直线
在直线![]() 下方的二次函数图象上.设点
下方的二次函数图象上.设点![]() 的横坐标为
的横坐标为![]() .过点
.过点![]() 作
作![]() 于点
于点![]() 求线段
求线段![]() 的长关于
的长关于![]() 的函数解析式,并求线段
的函数解析式,并求线段![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com