
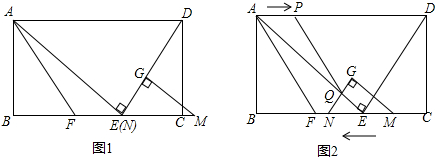
���� ��1�����ͼ1��ʾ��֤��QEMGΪƽ���ı��Σ����˶�·��QG=EM=12��tֵ����
��2�����ڷ��������ĵ�P����Rt��ABE�У�AB=12��BE=12$\sqrt{3}$���ɹ��ɶ����ã�AE=24�������Ǻ����Ķ���õ���AEB=30�㣬���sin��AEB=$\frac{1}{2}$��cos��AEB=$\frac{\sqrt{3}}{2}$������NE=t�����ǵõ�QE=NE•cos30��=$\frac{\sqrt{3}}{2}$t��AQ=AE-QE=24-$\frac{\sqrt{3}}{2}$t����APQ��ֱ�������Σ������ֿ��ܵ����Σ��١�APQ=90�㣬��ͼ2��ʾ�������ı���ABCD�Ǿ��Σ��õ�AD��BC�������PAQ=��AEB=30�㣬���ǵõ�cos��PAQ=cos30��=$\frac{AP}{AQ}$=$\frac{\sqrt{3}}{2}$�����t=$\frac{48\sqrt{3}}{11}$���ڵ���AQP=90��ʱ����ͼ3��ʾ��������֪�����õ�tan��GMN=$\frac{NG}{MG}$=$\frac{\sqrt{3}}{3}$�������GMN=30�㣬����ƽ���ߵ����ʵõ���GQE+��QGM=180�����N��G��Q���㹲�ߣ�����cos��PAQ=cos30��=$\frac{AQ}{AP}$���з���$\frac{24-\frac{\sqrt{3}}{2}t}{2t}$=$\frac{\sqrt{3}}{2}$�����ɵõ����ۣ�
���  �⣺��1����Rt��GMN�У�GN=6��GM=6$\sqrt{3}$��
�⣺��1����Rt��GMN�У�GN=6��GM=6$\sqrt{3}$��
��MN=12��
�����⣬��֪��G���˶���·ƽ����BC��
���ͼ1��ʾ������G��BC��ƽ���ߣ��ֱ�AE��AF�ڵ�Q��R��
�ߡ�AED=��EGM=90�㣬
��AE��GM��
���ı���QEMGΪƽ���ı��Σ�
��QG=EM=12��
��t=12�룻
��2�����ڷ��������ĵ�P��
��Rt��ABE�У�AB=12��BE=12$\sqrt{3}$���ɹ��ɶ����ã�AE=24��
���AEB=30�㣬��sin��AEB=$\frac{1}{2}$��cos��AEB=$\frac{\sqrt{3}}{2}$��
��NE=t����QE=NE•cos30��=$\frac{\sqrt{3}}{2}$t��AQ=AE-QE=24-$\frac{\sqrt{3}}{2}$t��
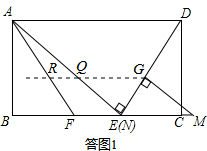
��APQ��ֱ�������Σ������ֿ��ܵ����Σ� �١�APQ=90�㣬��ͼ2��ʾ��
�١�APQ=90�㣬��ͼ2��ʾ��
���ı���ABCD�Ǿ��Σ�
��AD��BC��
���PAQ=��AEB=30�㣬
��cos��PAQ=cos30��=$\frac{AP}{AQ}$=$\frac{\sqrt{3}}{2}$��
��AP=2t��
��$\frac{2t}{24-\frac{\sqrt{3}}{2}t}$=$\frac{\sqrt{3}}{2}$��
��ã�t=$\frac{48\sqrt{3}}{11}$��
�ڵ���AQP=90��ʱ����ͼ3��ʾ��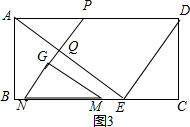
��NG=6��MG=6$\sqrt{3}$��
��tan��GMN=$\frac{NG}{MG}$=$\frac{\sqrt{3}}{3}$��
���GMN=30�㣬
��QE��GM��
���GQE+��QGM=180�㣬
���QGM=90�㣬
���QGM+��NGM=180�㣬
��N��G��Q���㹲�ߣ�
��cos��PAQ=cos30��=$\frac{AQ}{AP}$��
��$\frac{24-\frac{\sqrt{3}}{2}t}{2t}$=$\frac{\sqrt{3}}{2}$��
��ã�t=$\frac{16\sqrt{3}}{3}$��
������������t=$\frac{48\sqrt{3}}{11}$��$\frac{16\sqrt{3}}{3}$��ʱ�����ڵ�P��ʹ��APQ��ֱ�������Σ�
���� ���⿼���˾��ε����ʣ�ƽ���ߵ��ж������ʣ����Ǻ��������ɶ�����ƽ���ı��ε��ж������ʣ�����ؼ����������ͼ�ε��˶����̣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 12 | C�� | 18 | D�� | 24 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ����¥ǰ�IJм���ͨ����б�£���AB��ʾ������ͨ����3.2����¥����¥����¥��ĵ����0.4�ף���м���ͨ�����¶����½ǣ��ǶȾ�ȷ��1�䣬����������ֵ��ȷ��0.01����
��ͼ��һ����¥ǰ�IJм���ͨ����б�£���AB��ʾ������ͨ����3.2����¥����¥����¥��ĵ����0.4�ף���м���ͨ�����¶����½ǣ��ǶȾ�ȷ��1�䣬����������ֵ��ȷ��0.01�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com