
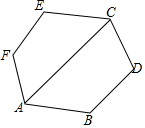
 如图,六边形的每个内角相等,且对角线AC平分∠FAB.
如图,六边形的每个内角相等,且对角线AC平分∠FAB.分析 (1)利用多边形内角和公式进行计算即可;
(2)首先证明∠ACD+∠D=180°,可得AC∥DB,再证明∠ACE+∠E=180°可得AC∥EF,进而可得EF∥BD.
解答 (1)解:∵六边形ABCDEF的各个内角都相等,
∴∠ECD=$\frac{180°(6-2)}{6}$=120°,
∵对角线AC平分∠FAB,
∴∠ACD=60°;
(2)证明:六边形的内角和为:(6-2)×180°=720°.
∵六边形ABCDEF的内角都相等,
∴每个内角的度数为:720°÷6=120°.
∵∠ACD=60°,
∴∠ACD+∠D=180°,
∴AC∥DB,
又∵∠ACD=60°,
∴∠ACE=120°-60°=60°,
∴∠ACE+∠E=180°,
∴AC∥EF,
∴EF∥DB.
点评 此题主要考查了多边形内角和,以及平行线的判定,关键是掌握多边形内角和定理:(n-2)•180 (n≥3)且n为整数),以及平行线的判定定理:同旁内角互补,两直线平行.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 阅读纸质书籍的数量(本) | 3 | 7 | 11 | 15 |
| 人数 | 4 | 8 | 10 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$×4$\sqrt{2}$=12$\sqrt{2}$ | B. | $\sqrt{(-3)^{2}}$=-3 | C. | ($\sqrt{8}$-$\sqrt{3}$)×$\sqrt{6}$=4$\sqrt{3}$-9$\sqrt{2}$ | D. | (4$\sqrt{2}$-3$\sqrt{6}$)÷2$\sqrt{2}$=2-$\frac{3}{2}$$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com