
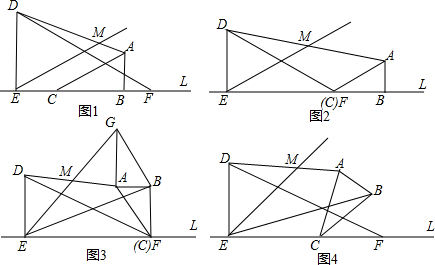
���� ��1����֤��AC��EM���ó�$\frac{DO}{OF}$=$\frac{DM}{AM}$��Ȼ����ݵȽǶԵȱߵó�OE=OF��OD=OE���Ӷ����OD=OF������֤��AM=DM��
��2���ٸ���30��ǵ�ֱ�������ε��������$\frac{BG}{BE}$=$\frac{AB}{BF}$��Ȼ��֤�á�ABG=��EBF���������������Ƶ��ж�����֤�á�ABG�ס�CBE����ͨ����ֱ�����������EF=2$\sqrt{3}$��BF=$\sqrt{3}$��Ȼ����ݡ�ABG�ס�CBE����Ӧ�߳ɱ����ó�$\frac{AG}{EF}$=$\frac{AB}{BF}$���������AG�ij���
��3����B����BG��BE����EM���ӳ�����G������AG����֤����ABG�ס�CBE���̶��Ƴ�AG��DE����AGM�ס�DEM���������������ε����ʼ��ɵó��𰸣�
���  ��1���⣺�ǣ�
��1���⣺�ǣ�
��ͼ2���ߡ�MEB=��ACB=30�㣬
��AC��EM��
��$\frac{DO}{OF}$=$\frac{DM}{AM}$
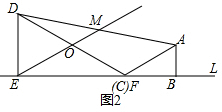
�ߡ�MEB=��DFE=30�㣬
��OE=OF��
�ߡ�DEF=90�㣬��MEB=30�㣬
���DEM=��EDF=60�㣬
��OD=OE��
��OD=OF��
��AM=DM��
��2����֤�����ߡ�EBG=90�㣬��ABC=90�㣬
���EBG=��ABC��
���EBG-��ABE=��ABC-��ABE������ABG=��EBF��
�ߡ�GEB=30���EBG=90�㣬
��tan30��=$\frac{BG}{BE}$��
��RT��ABC�У���ACB=30�㣬
��tan30��=$\frac{AB}{BF}$��
��$\frac{BG}{BE}$=$\frac{AB}{BF}$��
���ABG�ס�CBE��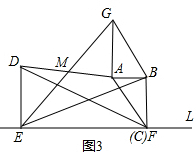 �ڽ⣺��ͼ3����RT��DEF�У�DE=2����DFE=30�㣬
�ڽ⣺��ͼ3����RT��DEF�У�DE=2����DFE=30�㣬
��EF=$\frac{DE}{tan30��}$=2$\sqrt{3}$��
��RT��ABF�У�AB=1����AFB=30�㣬
��BF=$\frac{AB}{tan30��}$=$\sqrt{3}$��
�ߡ�ABG�ס�CBE��
��$\frac{AG}{EF}$=$\frac{AB}{BF}$����$\frac{AG}{2\sqrt{3}}$=$\frac{1}{\sqrt{3}}$��
��AG=2��
��3���⣺��ͼ4��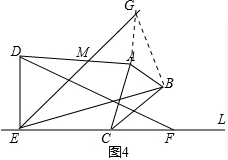 ��B����BG��BE����EM���ӳ�����G������AG��
��B����BG��BE����EM���ӳ�����G������AG��
ͬ��2������֤����ABG�ס�CBE��
���BEF=��AGB��$\frac{AG}{EC}$=$\frac{AB}{BC}$=$\frac{\sqrt{3}}{3}$��
��AG=$\frac{\sqrt{3}}{3}$EC=$\frac{\sqrt{3}}{3}$x��
���MEB=30�㣬
���DEM+��BEF=60�㣬��EGA+��AGB=60��
�ߡ�BEF=��AGB��
���DEM=��EGA��
��DE��AG��
���AGM�ס�DEM��
��$\frac{AM}{DM}$=$\frac{AG}{DE}$=$\frac{\frac{\sqrt{3}}{3}x}{2}$=$\frac{\sqrt{3}}{6}$x��
���� ���⿼�����������ۺ��⣬�漰�����������ε��ж������ʡ�ƽ���ߵ����ʡ���ת�����ʼ�ֱ�������ε����ʣ������֪ʶ��Ƚ϶࣬�ѶȽϴ��������ո�������֪ʶ���ǽ���Ĺؼ���


 Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
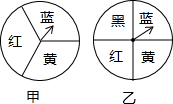 ��ͼ���мס�������ת�̣�ÿ��ת���ϸ������ε�Բ�ĽǶ���ȣ�������ת�̷ֱ�����ת��һ�Σ���ת��ָ�����ڷֽ�����ʱ������ת����
��ͼ���мס�������ת�̣�ÿ��ת���ϸ������ε�Բ�ĽǶ���ȣ�������ת�̷ֱ�����ת��һ�Σ���ת��ָ�����ڷֽ�����ʱ������ת�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����O�ǡ�ABC�����Բ��AB�ǡ�O��ֱ����IΪ��ABC�����ģ�AI���ӳ��߽�BC��D����OI��AD����tan��CAD��ֵΪ��������
��ͼ����O�ǡ�ABC�����Բ��AB�ǡ�O��ֱ����IΪ��ABC�����ģ�AI���ӳ��߽�BC��D����OI��AD����tan��CAD��ֵΪ��������| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{2}}{2}$ | C�� | $\frac{\sqrt{5}}{5}$ | D�� | $\frac{\sqrt{5}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
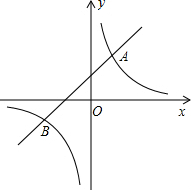 ��ͼ����֪һ�κ���y1=kx+b�뷴��������y2=$\frac{m}{x}$��ͼ����A��2��4����B��-4��n�����㣮
��ͼ����֪һ�κ���y1=kx+b�뷴��������y2=$\frac{m}{x}$��ͼ����A��2��4����B��-4��n�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ax2+bx+c=0 | B�� | x2-2=��x+3��2 | C�� | 2x+3x-5=0 | D�� | x2-1=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | M��N | B�� | M��N | C�� | M��N | D�� | M��N |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com