
����Ŀ�������������٣�ij��ҵ����������Ͷ�빲�����������г��������絥�����綯������2000������֪ÿ�����������ɱ�380Ԫ��ÿ̨�����絥���ɱ�1500Ԫ��2������������1�������絥��ÿ��ë��31Ԫ��4������������3�������絥��ÿ��ë��81Ԫ��
��1���������������絥��ÿ��ÿ���ֱ����ӯ������Ԫ��
��2��Ϊ����Ͷ�ʻر��ʣ�����ҵ�ƻ�Ͷ��ɱ�������174��Ԫ��ÿ�ܵ�ë��������23050Ԫ����Ҫ��Ͷ��ĵ�������Ϊ10�ı����������оٳ�����Ͷ���ʽ���
���𰸡���1���������������絥��ÿ��ÿ���ֱ����ӯ��6Ԫ��19Ԫ����2��������.
��������
��1�����蹲�����������綯��ÿ��ÿ���ֱ����ӯ��xԪ��yԪ�����������г���������⼴�ɣ�
��2����Ͷ��Ĺ�����������Ϊ10n�������������г�����n�IJ���ʽ�飬�������ʽ��Ľ⼯���ٽ��nΪ��Ȼ��ȷ��n�ľ���ֵ�����д����������.
�⣺�蹲������ÿ��ÿ������ӯ��xԪ�������絥��ÿ��ÿ������ӯ��yԪ��
�������⣬��![]()
���![]()
�𣺹������������絥��ÿ��ÿ���ֱ����ӯ��6Ԫ��19Ԫ.
��2����Ͷ��Ĺ�����������Ϊ10n����
��Ͷ��Ĺ����絥������Ϊ��2000��10n����.
���������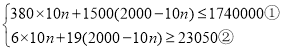
�ⲻ��ʽ�ٵã�![]() ��
��
�ⲻ��ʽ�ڵã�![]() ��
��
��ԭ����ʽ��Ľ⼯Ϊ![]() .
.
������֪nΪ��Ȼ����
��n��ȡ��ֵΪ113,114,115.
��n=113ʱ��10��113=1130��������2000��1130=870��������
��n=114ʱ��10��114=1140��������2000��1140=860��������
��n=115ʱ��10��115=1150��������2000��1150=850������.
��Ͷ���ʽ�Ϊ��
����һ��Ͷ�빲������1130���������絥��870����
��������Ͷ�빲������1140���������絥��860����
��������Ͷ�빲������1150���������絥��850��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=(2m+4)x����
(1)mΪ��ֵʱ������ͼ����һ�������ޣ�
(2)mΪ��ֵʱ��y��x���������С��
(3)mΪ��ֵʱ����(1��3)�ڸú�����ͼ���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC����D��E�ֱ��DZ�AB��AC���е㣬��F��BC���ϣ�����DE��DF��EF��������������һ�������������ж���FCE����EDFȫ�ȣ� ��
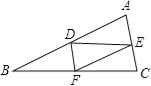
A. ��A=��DFE B. BF=CF C. DF��AC D. ��C=��EDF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
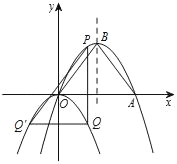
����Ŀ����ͼ��������y=��![]() x2+bx+c����ԭ��͵�A��6��0��������Գ��ύ�ڵ�B��P��������y=��
x2+bx+c����ԭ��͵�A��6��0��������Գ��ύ�ڵ�B��P��������y=��![]() x2+bx+c��һ���㣬����x���Ϸ�������P��x��Ĵ��߽���������y=��
x2+bx+c��һ���㣬����x���Ϸ�������P��x��Ĵ��߽���������y=��![]() ��x��h��2��hΪ�������ڵ�Q������Q��PQ�Ĵ��߽���������y=��
��x��h��2��hΪ�������ڵ�Q������Q��PQ�Ĵ��߽���������y=��![]() ��x��h��2�ڵ�Q���������Q�غϣ�������PQ�������P�ĺ�����Ϊm��
��x��h��2�ڵ�Q���������Q�غϣ�������PQ�������P�ĺ�����Ϊm��
��1����������y=��![]() x2+bx+c�ĺ�����ϵʽ����B�����ꣻ
x2+bx+c�ĺ�����ϵʽ����B�����ꣻ
��2����h=0ʱ��
����֤�� ![]() ��
��
������PQQ������OAB�ص�����ͼ�ε��ܳ�Ϊl����l��m֮��ĺ�����ϵʽ��
��3����h��0ʱ���Ƿ���ڵ�P��ʹ�ı���OAQQ��Ϊ���Σ������ڣ���ֱ��д��h��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ�����װ��ֻ����ɫ��ͬ�ĺڡ���������50����Сӱ������ʵ�飬�����������������Ⱥ�����������һ���������ɫ���ٰ����Żغ����У������ظ��������̣��±��������е�һ��ͳ�����ݣ�
������Ĵ��� | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
��������Ĵ��� | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
��������ĸ��� | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
��1������Ƶ�![]() �ܴ�ʱ�����������Ƶ�ʽ���ӽ�______������ȷ��0.1����
�ܴ�ʱ�����������Ƶ�ʽ���ӽ�______������ȷ��0.1����
��2�����������һ�Σ���������ĸ���P��������______��
��3���Թ���������ɫ�����ж��ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����Ӧ�������У����Ŀ�꣬ijУ�ƻ�ΪѧУ����ӹ���һ��������֪����2��AƷ�Ƶ������3��BƷ�Ƶ�������380Ԫ������4��AƷ�Ƶ������2��BƷ�Ƶ�������360Ԫ��

��1����A��B����Ʒ�Ƶ�����ĵ��ۣ�
��2�����У����20��AƷ�Ƶ������2��BƷ�Ƶ�������ܷ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
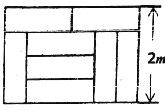
����Ŀ����ͼ,8����ͬ��С�����ε�שƴ��һ������,
��1��ÿ��С�����ε�ש�ij��Ϳ��ֱ��Ƕ���?(Ҫ���з�������н��)
��2��С������һ�����Ϊ7ƽ�������������������űߵķ���ü���һ���µij�����������������ס��鳤����ľ�������С����һ�㣬���ܼ�������Ҫ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ƻ�����һ���ס���������ߣ���֪һ��������ߵĽ�����һ��������ߵĽ��۵ĺ�Ϊ40Ԫ����90Ԫ����������ߵļ�������150Ԫ����������ߵļ�����ͬ��
��1����ÿ�����֡�������ߵĽ��۷ֱ��Ƕ���Ԫ��
��2���̳��ƻ������ס���������߹�48�������м�����ߵļ�������������ߵļ������̳������˴ν��������ʽ���1000Ԫ�����̳����м��ֽ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
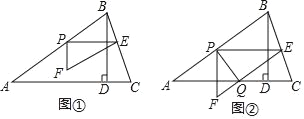
����Ŀ����ͼ�٣��������ABC�У�AB=5��tanC=3��BD��AC�ڵ�D��BD=3����P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���AB���յ�B�˶�������P��PE��AC����BC�ڵ�E����PEΪ����Rt��PEF��ʹ��EPF=90������F�ڵ�P���·�����EF��AB������PEF����ABD�ص�����ͼ�ε����ΪS��ƽ����λ����S��0������P���˶�ʱ��Ϊt���룩��t��0����
��1�����߶�AC�ij���
��2������PEF����ABD�ص�����ͼ��Ϊ�ı���ʱ����S��t֮��ĺ�����ϵʽ��
��3������EF���AC���ڵ�Q������PQ����ͼ����
�ٵ�PQ����PEF������ֳ�1��2������ʱ����AP�ij���
��ֱ��д��PQ�Ĵ�ֱƽ���߾�����ABC�Ķ���ʱt��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com