
分析 (1)根据已知的式子,得出$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,然后根据此规律进行解答即可;
(2)根据规律$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,再把要求的式子进行整理即可得出答案;
(3)先把分母进行因式分解,再根据找出的规律得出$\frac{1}{2(x-3)}$-$\frac{1}{2(x-1)}$=$\frac{1}{x-1}$,然后求解即可.
解答 解解:(1)$\frac{1}{x(x+1)}$+$\frac{1}{(x+1)(x+2)}$+$\frac{1}{(x+2)(x+3)}$+…+$\frac{1}{(x+8)(x+9)}$=$\frac{1}{x}$-$\frac{1}{x+1}$+$\frac{1}{x+1}$-$\frac{1}{x+2}$+…+$\frac{1}{x+8}$-$\frac{1}{x-9}$=$\frac{1}{x}$-$\frac{1}{x-9}$=$\frac{9}{x(x+9)}$;
(2)$\frac{1}{(x-2)(x-3)}$-$\frac{2}{(x-1)(x-3)}$+$\frac{1}{(x-1)(x-2)}$=$\frac{1}{x-3}$-$\frac{1}{x-2}$-$\frac{1}{x-3}$+$\frac{1}{x-1}$+$\frac{1}{x-2}$-$\frac{1}{x-1}$=0;
(3)$\frac{1}{{x}^{2}-5x+6}$-$\frac{1}{{x}^{2}-4x+3}$+$\frac{1}{{x}^{2}-3x+2}$
=$\frac{1}{(x-2)(x-3)}$-$\frac{1}{(x-1)(x-3)}$+$\frac{1}{(x-1)(x-2)}$
=$\frac{1}{x-3}$-$\frac{1}{x-2}$-[$\frac{1}{2}$($\frac{1}{x-3}$-$\frac{1}{x-1}$)]+$\frac{1}{x-2}$-$\frac{1}{x-1}$
=$\frac{1}{2(x-3)}$-$\frac{1}{2(x-1)}$=$\frac{1}{x-1}$,
解得:x=4,
经检验x=4是原方程的解.
点评 此题考查了分式的加减及解分式方程,关键是找出式子的规律.然后用得出的规律得出所求的值.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.求:
如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
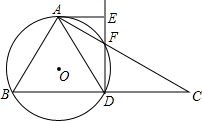 如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.
如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是( )
如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是( )| A. | 10尺 | B. | 11尺 | C. | 12尺 | D. | 13尺 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com