Question

1．某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：
操作发现：
在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，
则下列结论正确的是①②③④⑤．（填序号即可）
①AF=AG=$\frac{1}{2}$AB；②MD=ME；③四边形AFMG是菱形；④整个图形是轴对称图形；⑤MD⊥ME．
数学思考：
在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD和ME，则MD和ME具有怎样的数量关系和位置关系？请给出证明过程；
类比探索：
在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD和ME，试判断△MED的形状．答：等腰直角三角形．
拓展延伸：
在三边互不相等的△ABC中（见备用图），仍分别以AB和AC为斜边，向△ABC的内侧作（非等腰）直角三角形ABD和（非等腰）直角三角形ACE，M是BC的中点，连接MD和ME，要使MD和ME仍具备图2中的数量关系，你认为需增加一个什么样的条件？（限用题中字母表示）．答：∠BAD=∠CAE或∠BAD+∠CAE=∠BAC．

Answer 1

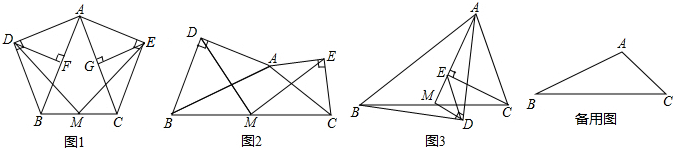
分析 操作发现：由条件可以通过三角形全等和轴对称的性质，直角三角形的性质就可以得出结论；
数学思考：如图2，取AB、AC的中点F、G，连接DF，MF，EG，MG，根据三角形的中位线的性质和等腰直角三角形的性质就可以得出四边形AFMG是平行四边形，从而得出△DFM≌△MGE，根据其性质就可以得出结论；
类比探索：如图3，取AB、AC的中点F、G，连接DF，MF，EG，MG，DF和MG相交于H，根据三角形的中位线的性质K可以得出△DFM≌△MGE，由全等三角形的性质就可以得出结论；
拓展延伸：如图4，作直角三角形ADB和直角三角形AEC，∠ADB=∠AEC=90°，当∠BAD=∠CAE时，作AB、AC的中点F、G，连接DF，MF，EG，MG，DF和MG相交于H，根据三角形的中位线的性质K可以得出△DFM≌△MGE，由全等三角形的性质就可以得出结论DM=EM．

解答 解：操作发现：∵△ADB和△AEC是等腰直角三角形，
∴∠ABD=∠DAB=∠ACE=∠EAC=45°，∠ADB=∠AEC=90°
在△ADB和△AEC中，
$\left\{\begin{array}{l}{∠ADB=∠AEC}\\{∠ABD=∠ACE}\\{AB=AC}\end{array}\right.$，
∴△ADB≌△AEC（AAS），
∴BD=CE，AD=AE，
∵DF⊥AB于点F，EG⊥AC于点G，
∴AF=BF=DF=$\frac{1}{2}$AB，AG=GC=GE=$\frac{1}{2}$AC．
∵AB=AC，
∴AF=AG=$\frac{1}{2}$AB，故①正确；
∵M是BC的中点，
∴BM=CM．
∵AB=AC，
∴∠ABC=∠ACB，
∴∠ABC+∠ABD=∠ACB+∠ACE，
即∠DBM=∠ECM．
在△DBM和△ECM中，
$\left\{\begin{array}{l}{BD=CE}\\{∠DBM=∠ECM}\\{BM=CM}\end{array}\right.$，
∴△DBM≌△ECM（SAS），
∴MD=ME．故②正确；
连接AM、FM、GM，如图1所示：
∵AB=AC，M是BC的中点，
∴AM⊥BC，
∴∠AMB=∠AMC=90°，
又∵AF=BF，AG=CG，
∴FM=$\frac{1}{2}$AB=AF，GM=$\frac{1}{2}$AC=AG，
∴AF=FM=GM=AG，
∴四边形AFMG是菱形，
故③正确； 
连接AM，根据前面的证明可以得出将图形1，沿AM对折左右两部分能完全重合，
∴整个图形是轴对称图形，故④正确．
∵AB=AC，BM=CM，
∴AM⊥BC，
∴∠AMB=∠AMC=90°，
∵∠ADB=90°，
∴四边形ADBM四点共圆，
∴∠AMD=∠ABD=45°．
∵AM是对称轴，
∴∠AME=∠AMD=45°，
∴∠DME=90°，
∴MD⊥ME，故⑤正确，
故答案为：①②③④⑤．

数学思考：MD=ME，
理由：如图2，取AB、AC的中点F、G，连接DF，MF，EG，MG，
∴AF=$\frac{1}{2}$AB，AG=$\frac{1}{2}$AC．
∵△ABD和△AEC是等腰直角三角形，
∴DF⊥AB，DF=$\frac{1}{2}$AB，EG⊥AC，EG=$\frac{1}{2}$AC，
∴∠AFD=∠AGE=90°，DF=AF，GE=AG．
∵M是BC的中点，
∴MF∥AC，MG∥AB，
∴四边形AFMG是平行四边形，
∴AG=MF，MG=AF，∠AFM=∠AGM．
∴MF=GE，DF=MG，∠AFM+∠AFD=∠AGM+∠AGE，
∴∠DFM=∠MGE．
在△DFM和△MGE中，
$\left\{\begin{array}{l}{MF=EG}\\{∠DFM=∠MGE}\\{DF=MG}\end{array}\right.$，
∴△DFM≌△MGE（SAS），
∴DM=ME；

类比探索：如图3，取AB、AC的中点F、G，连接DF，MF，EG，MG，
∵点M、F、G分别是BC、AB、AC的中点，
∴MF∥AC，MF=$\frac{1}{2}$AC，MG∥AB，MG=$\frac{1}{2}$AB，
∴四边形MFAG是平行四边形，
∴MG=AF，MF=AG．∠AFM=∠AGM．
∵△ADB和△AEC是等腰直角三角形，
∴DF=AF，GE=AG，∠AFD=∠BFD=∠AGE=90°
∴MF=EG，DF=MG，∠AFM-∠AFD=∠AGM-∠AGE，
即∠DFM=∠MGE．
在△DFM和△MGE中
$\left\{\begin{array}{l}{MF=EG}\\{∠DFM=∠MGE}\\{DF=MG}\end{array}\right.$，
∴△DFM≌△MGE（SAS），
∴MD=ME，∠MDF=∠EMG．
∵MG∥AB，
∴∠MHD=∠BFD=90°，
∴∠HMD+∠MDF=90°，
∴∠HMD+∠EMG=90°，
即∠DME=90°，
∴△DME为等腰直角三角形；
故答案是：等腰直角三角形；

拓展延伸：如图4，△ADB和△AEC是直角三角形，∠ADB=∠AEC=90°，当∠BAD=∠CAE时，DM=EM．
理由：取AB、AC的中点F、G，连接DF，MF，EG，MG，
∴MF=$\frac{1}{2}$AC，MF∥AC，MG=$\frac{1}{2}$AB，MG∥AB，
∴四边形AFMG是平行四边形，
∴MF=AG，MG=AF，∠AFM=∠AGM．
∵∠ADB=∠AEC=90°，
∴DF=AF，EG=AG，
∴DF=MG，MF=EG，∠FDA=∠DAF，∠GEA=∠GAE．
∵∠BAD=∠CAE，
∴∠FDA=∠DAF=∠AEG=∠GAE，
∴∠AFD=∠AGE，
∴∠AFD-∠AFM=∠AGE-∠AGM，
即∠DFM=∠MGE．
在△DFM和△MGE中，
$\left\{\begin{array}{l}{DF=MG}\\{∠DFM=∠MGE}\\{MF=EG}\end{array}\right.$，
∴△DFM≌△MGE（SAS），
∴DM=ME．
故答案是：∠BAD=∠CAE或∠BAD+∠CAE=∠BAC．

点评 本题考查了等腰直角三角形的性质的运用，等腰三角形的性质的运用，全等三角形的判定及性质的运用，三角形的中位线的性质的运用，直角三角形的斜边上的中线的性质的运用，平行四边形的判定及性质的运用，解答时根据三角形的中位线的性质制造全等三角形是解答本题的关键．