
��ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ(��3��0)��(0��4)��������y��![]() x2��bx��c����B�㣬�Ҷ�����ֱ��x��
x2��bx��c����B�㣬�Ҷ�����ֱ��x��![]() �ϣ�
�ϣ�
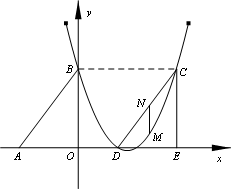
(1)�������߶�Ӧ�ĺ�����ϵʽ��
(2)����DCE���ɡ�ABO��x������ƽ�Ƶõ��ģ����ı���ABCD������ʱ�����жϵ�C�͵�D�Ƿ��ڸ��������ϣ���˵�����ɣ�
(3)��M����CD����ֱ���·����������ϵ�һ�����㣬����M��MNƽ����y�ύCD�ڵ�N�����M�ĺ�����Ϊt��MN�ij���Ϊl����l��t֮��ĺ�����ϵʽ������lȡ���ֵʱ����M�����꣮
|
�����⣺(1)�����⣬�������������߶�Ӧ�ĺ�����ϵʽΪ ������ ������ ��������������ϵʽΪ�� ����(2)��Rt��ABO�У�OA��3��OB��4�� ������ �������ı���ABCD������ ������BC��CD��DA��AB��5����(5��) ������C��D���������ֱ���(5��4)��(2��0)����(6��) ������ ������ �������C�͵�D�������������ϡ���(7��) ����(3)��ֱ��CD��Ӧ�ĺ�����ϵʽΪ ���� ������ã� ������ ������MN��y�ᣬM��ĺ�����Ϊt�� ������N��ĺ�����ҲΪt�� ������ ������ ������ ������ʱ��M������Ϊ(
|


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
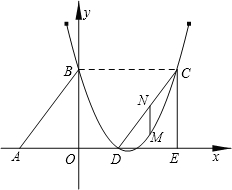 ��ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ��-3��0������0��4����������y=
��ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ��-3��0������0��4����������y=| 2 |
| 3 |
| 5 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| k |
| x |
 ���ڵ������Ľ��㣬AB��x����B����S��ABO=
���ڵ������Ľ��㣬AB��x����B����S��ABO=| 5 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ԭ�㣬A��B���������ֱ�Ϊ��-3��0������0��4����������y=
��ԭ�㣬A��B���������ֱ�Ϊ��-3��0������0��4����������y=| 2 |
| 3 |
| 5 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��Rt��ABO�Ķ���A�Ƿ���������y=
��ͼ��Rt��ABO�Ķ���A�Ƿ���������y=| k |
| x |
| 3 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��Rt��ABO�Ķ���A��˫����y=
��ͼ��Rt��ABO�Ķ���A��˫����y=| k |
| x |
| 3 |
| 2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com