
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,AG交CD于K,E为CD延长线上一点,且EK=EG,EG的延长线交AB的延长线于F. 
(1)求证:EF为⊙O的切线;
(2)若DK=2HK=AK,CH= ![]() ,求图中阴影部分的面积S.
,求图中阴影部分的面积S.
【答案】
(1)证明:连接OG,如图1所示:

∵弦CD⊥AB于点H,
∴∠AHK=90°,
∴∠HKA+∠KAH=90°,
∵EG=EK,
∴∠EGK=∠EKG,
∵∠HKA=∠GKE,
∴∠HAK+∠KGE=90°,
∵AO=GO,
∴∠OAG=∠OGA,
∴∠OGA+∠KGE=90°,
∴GO⊥EF,
∴EF是⊙O的切线
(2)解:∵CD⊥AB,
∴DH=CH= ![]() ,
,
∵DK=2HK=AK,
∴∠HAK=30°,HK= ![]() DH=
DH= ![]() ,
,
∴AH= ![]() HK=
HK= ![]() ,
,
连接OD,如图2所示:

设⊙O的半径为R,
在Rt△ODH中,由勾股定理得:( ![]() )2+(R﹣
)2+(R﹣ ![]() )2=R2,
)2=R2,
解得:R=2 ![]() ,
,
∴OH=OA﹣AH= ![]() =
= ![]() OD,
OD,
∴∠ODH=30°,△ODH的面积= ![]() OHDH=
OHDH= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
∴∠DOH=60°,
∴∠BOD=120°,
∴扇形OBGD的面积= ![]() =
= ![]() ,
,
∵OA=OG,
∴∠OGA=∠HAK=30°,
∴∠EGK=90°﹣30°=60°,
又∵EK=EG,
∴△GEK是等边三角形,
∴∠E=60°,
∴∠F=90°﹣60°=30°,
∵GO⊥EF,
∴OF=2OG=4 ![]() ,
,
∴HF=OH+OF=5 ![]() ,
,
∴HE= ![]() HF=
HF= ![]()
∴△EFH的面积= ![]() HFHE=
HFHE= ![]() ×5
×5 ![]() ×
× ![]() =
= ![]() ,
,
∴图中阴影部分的面积S= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]()
【解析】(1)连接OG,首先证明∠EGK=∠EKG,再证明∠HAK+∠KGE=90°,进而得到∠OGA+∠KGE=90°即GO⊥EF,进而证明EF是⊙O的切线;(2)与已知条件得出∠HAK=30°,HK= ![]() DH=
DH= ![]() ,AH=
,AH= ![]() HK=
HK= ![]() ,连接OD,设⊙O的半径为R,在Rt△ODH中,由勾股定理得出方程,解方程求出半径,得出OH=
,连接OD,设⊙O的半径为R,在Rt△ODH中,由勾股定理得出方程,解方程求出半径,得出OH= ![]() OD,求出∠ODH=30°,△ODH的面积=
OD,求出∠ODH=30°,△ODH的面积= ![]() ,再求出∠BOD=120°,得出扇形OBGD的面积=
,再求出∠BOD=120°,得出扇形OBGD的面积= ![]() ,证明△GEK是等边三角形,求出OF=2OG=4
,证明△GEK是等边三角形,求出OF=2OG=4 ![]() ,得出HF=OH+OF=5
,得出HF=OH+OF=5 ![]() ,求出HE=
,求出HE= ![]() ,计算出△EFH的面积,即可得出结果.
,计算出△EFH的面积,即可得出结果.
【考点精析】关于本题考查的垂径定理和扇形面积计算公式,需要了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,由下列条件可判定哪两条直线平行,并说明根据.

(1)∠1=∠2,________________________.
(2)∠A=∠3,________________________.
(3)∠ABC+∠C=180°,________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明:如图,已知![]() ,
,![]() ,
,![]() .
.
求证:![]() .
.

证明:![]() ,
,![]() (已知)
(已知)
![]() ,
,![]() (_____________________)
(_____________________)
![]() (等量代换)
(等量代换)
![]() (_______________________)
(_______________________)
![]() (__________________________)
(__________________________)
又![]() (已知)
(已知)
![]() _______
_______![]() ________(等量代换)
________(等量代换)
![]() (_____________________________)
(_____________________________)
![]() (____________________).
(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
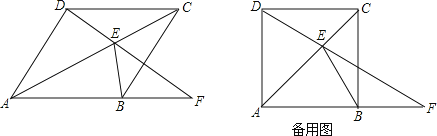
【题目】如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.
(1)求证:∠AFD=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC三条边的长度分别是![]() ,
,![]() ,
,![]() ,记△ABC的周长为C△ABC.
,记△ABC的周长为C△ABC.
(1)当x=2时,△ABC的最长边的长度是 (请直接写出答案);
(2)请求出C△ABC(用含x的代数式表示,结果要求化简);
(3)我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式:S=![]() .其中三角形边长分别为a,b,c,三角形的面积为S.
.其中三角形边长分别为a,b,c,三角形的面积为S.
若x为整数,当C△ABC取得最大值时,请用秦九韶公式求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,随机抽取其中32名学生两次考试考分等级制成统计图(如图),试回答下列问题:
(1)这32名学生经过培训,考分等级“不合格”的百分比由________下降到________;
(2)估计该校640名学生,培训后考分等级为“合格”与“优秀”的学生共有多少名.

查看答案和解析>>
科目:初中数学 来源: 题型:
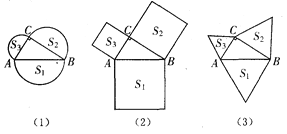
【题目】如图(1),分别以直角△ABC的三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难说明S1=S2+S3。(1)如图(2),分别以直角△ABC三边为一边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?(2)如图(3),若分别以直角△ABC三边为一边向外作三个正三角形,其面积分别用S1、S2、S3表示,试确定S1、S2、S3之间的关系并加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的边OA,OC分别在x轴、y轴上,点B坐标为(4,t)(t>0),二次函数y=x2+bx(b<0)的图象经过点B,顶点为点D.
(1)当t=12时,顶点D到x轴的距离等于;
(2)点E是二次函数y=x2+bx(b<0)的图象与x轴的一个公共点(点E与点O不重合),求OEEA的最大值及取得最大值时的二次函数表达式;
(3)矩形OABC的对角线OB、AC交于点F,直线l平行于x轴,交二次函数y=x2+bx(b<0)的图象于点M、N,连接DM、DN,当△DMN≌△FOC时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com