
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() ,以下结论:①
,以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() 。其中正确的结论的序号为___________。
。其中正确的结论的序号为___________。

【答案】③④
【解析】
作AP⊥AC交CE的延长线于P,连接CH.构造全等三角形,证明△CAP≌△BCG(ASA),△EAG≌△EAP(SAS),即可分步判断①②③,利用四点共圆可以证明④正确.
解:如图,作AP⊥AC交CE的延长线于P,连接CH.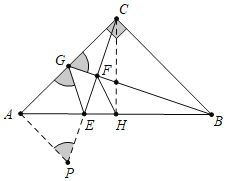
∵CE⊥BG,
∴∠CFB=∠ACB=90°,
∵∠ACE+∠BCE=90°,∠CBG+∠BCE=90°,
∴∠ACE=∠CBG,
∵BG是△ABC的中线,AB>BC,
∴∠ABG≠∠CBG,
∴∠ACE≠∠ABG,故①错误,
∵∠ACP=∠CBG,AC=BC,∠CAP=∠BCG=90°,
∴△CAP≌△BCG(ASA),
∴CG=PA=AG,∠BGC=∠P,
∵AG=AP,∠EAG=∠EAP=45°,AE=AE,
∴△EAG≌△EAP(SAS),
∴∠AGE=∠P,
∴∠AGE=∠CGB,故③正确,
∵![]() ,
,
∴△ABC是等腰直角三角形,
∴AC=BC=10,
∴AG=CG=5,
∴![]() ,
,
∵![]() ,
,
∴![]() ,故②错误,
,故②错误,
∵CA=CB,∠ACB=90°,AH=HB,
∴∠BCH=∠ACH=45°,
∵∠CFB=∠CHB=90°,
∴C,F,H,B四点共圆,
∴∠HFB=∠BCH=45°,
∴∠EFH=∠HFB=45°,
∴FH平分∠BFE,故④正确,
综上所述,正确的只有③④.
故答案为:③④


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的角平分线相交于点
的角平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() .下列五个结论:其中正确的有( )
.下列五个结论:其中正确的有( )
(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 到
到![]() 各边的距离都相等;(4)设
各边的距离都相等;(4)设![]() ,若
,若![]() ,则
,则![]() ;(5)
;(5)![]() .( )
.( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB═![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为![]() .
.
(1)求反比例函数的解析式;
(2)求直线EB的解析式;
(3)求S△OEB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个圆柱形玻璃杯高![]() ,底面周长为
,底面周长为![]() ,有一只蚂蚁在一侧距下底
,有一只蚂蚁在一侧距下底![]() 的外侧
的外侧![]() 点,与点
点,与点![]() 正对的容器内侧距下底
正对的容器内侧距下底![]() 的
的![]() 点处有一饭粒,蚂蚁想吃
点处有一饭粒,蚂蚁想吃![]() 处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________
处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________![]() 。
。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为1的等边△ABC的边AB上一点P作PE⊥AC于点E,Q为BC延长线上一点,当PA=CQ时,连接PQ交AC于点D,则DE的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求:
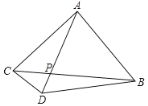
(1)∠BDC的度数,
(2)△ABD的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示.
(1)写出三角形③的顶点坐标.
(2)通过平移由三角形③能得到三角形④吗?
(3)根据对称性由三角形③可得三角形①,②,它们的顶点坐标各是什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com