

分析 由四边形ABCB1是正方形,得到AB=AB1,AB∥CB1,于是得到AB∥A1C,根据平行线的性质得到∠CA1A=30°,解直角三角形得到A1B1=$\sqrt{3}$,AA1=2,同理:A2A3=2($\sqrt{3}$)2,A3A4=2($\sqrt{3}$)3,找出规律AnAn+1=2($\sqrt{3}$)n,答案即可求出.
解答 解:∵四边形ABCB1是正方形,
∴AB=AB1,AB∥CB1,
∴AB∥A1C,
∴∠CA1A=30°,
∴A1B1=$\sqrt{3}$,AA1=2,
∴A1B2=A1B1=$\sqrt{3}$,
∴A1A2=2$\sqrt{3}$,
同理:A2A3=2($\sqrt{3}$)2,
A3A4=2($\sqrt{3}$)3,
…
∴AnAn+1=2($\sqrt{3}$)n,
∴A2015A2016=2($\sqrt{3}$)2015,
故答案为:2($\sqrt{3}$)2015.
点评 本题考查了正方形的性质,含30°直角三角形的性质,平行线的性质,熟记各性质并求出后一个正方形的边长是前一个正方形的边长的$\sqrt{3}$倍是解题的关键.


科目:初中数学 来源: 题型:选择题
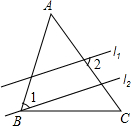 如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=55°,则∠2的大小为( )
如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=55°,则∠2的大小为( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
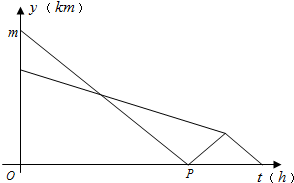 某部队凌晨5:00乘车从住宿地匀速赶往离住宿地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6:00到达B处后,空车原速返回接应先遣分队于6:40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图所示.
某部队凌晨5:00乘车从住宿地匀速赶往离住宿地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6:00到达B处后,空车原速返回接应先遣分队于6:40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{5}{7}$+$\frac{2}{7}$=1 | B. | 3÷$\frac{5}{4}$×$\frac{4}{5}$=3÷1=3 | C. | -7-2×5=-9×5=-45 | D. | 0-(-22)=22 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
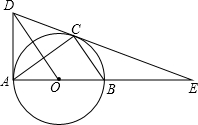 如图,△ABC内接于⊙O,AB为直径,E为AB延长线上的点,作OD∥BC交EC的延长线于点D,连接AD.
如图,△ABC内接于⊙O,AB为直径,E为AB延长线上的点,作OD∥BC交EC的延长线于点D,连接AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com