
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
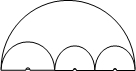 如图,两只蚂蚁同时从甲地爬向乙地,一只蚂蚁沿着大半圆爬行,另一只蚂蚁沿着三个小半圆爬行,哪只蚂蚁先到达乙地?为什么?(两只蚂蚁的爬行速度相同).
如图,两只蚂蚁同时从甲地爬向乙地,一只蚂蚁沿着大半圆爬行,另一只蚂蚁沿着三个小半圆爬行,哪只蚂蚁先到达乙地?为什么?(两只蚂蚁的爬行速度相同).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
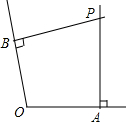 如图,任意画∠O,在∠O的两边上分别截取OA,OB,使OA=OB,过点A画OA的垂线,过点B画OB的垂线,设两条垂线相交于点P,点O在∠APB的平分线上吗?为什么?
如图,任意画∠O,在∠O的两边上分别截取OA,OB,使OA=OB,过点A画OA的垂线,过点B画OB的垂线,设两条垂线相交于点P,点O在∠APB的平分线上吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
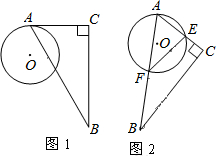 如图,将△ABC的顶点A放在⊙O上,现从AC与⊙O相切于点A(如图1)的位置开始,将△ABC绕着点A顺时针旋转,设旋转角为α(0°<α<120°),旋转后AC,AB分别与⊙O交于点E,F,连接EF(如图2).已知∠BAC=60°,∠C=90°,AC=8,⊙O的直径为8.在旋转过程中,有以下几个量:①弦EF的长 ②弧EF的长 ③∠AFE的度数 ④点O到EF的距离.其中不变的量是①②④(只填正确答案序号).
如图,将△ABC的顶点A放在⊙O上,现从AC与⊙O相切于点A(如图1)的位置开始,将△ABC绕着点A顺时针旋转,设旋转角为α(0°<α<120°),旋转后AC,AB分别与⊙O交于点E,F,连接EF(如图2).已知∠BAC=60°,∠C=90°,AC=8,⊙O的直径为8.在旋转过程中,有以下几个量:①弦EF的长 ②弧EF的长 ③∠AFE的度数 ④点O到EF的距离.其中不变的量是①②④(只填正确答案序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com