
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 为
为![]() 边的中点,将
边的中点,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为
的对应点为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 交于点
交于点![]() ,现有下列结论:①
,现有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④点
;④点![]() 为
为![]() 的外心.其中正确的是( )
的外心.其中正确的是( )

A.①④B.①③C.③④D.②④
科目:初中数学 来源: 题型:
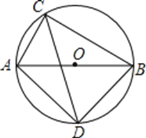
【题目】如图,⊙O的直径AB长为6,弦AC长为2,∠ACB的平分线交⊙O于点D.
(1)求BD的长;
(2)将△ADC绕D点顺时针方向旋转90°,请补充旋转后图形,并计算CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】时代天街某商场经营的某品牌书包,6月份的销售额为20000元,7月份因为厂家提高了出厂价,商场把该品牌书包售价上涨20%,结果销量减少50个,使得销售额减少了2000元.
(1)求6月份该品牌书包的销售单价;
(2)若6月份销售该品牌书包获利8000元,8月份商场为迎接中小学开学做促销活动,该书包在6月售价的基础上一律打八折销售,若成本上涨5%,则销量至少为多少个,才能保证8月份的利润比6月份的利润至少增长6.25%?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学概念
若点![]() 在
在![]() 的内部,且
的内部,且![]() 、
、![]() 和
和![]() 中有两个角相等,则称
中有两个角相等,则称![]() 是
是![]() 的“等角点”,特别地,若这三个角都相等,则称
的“等角点”,特别地,若这三个角都相等,则称![]() 是
是![]() 的“强等角点”.
的“强等角点”.
理解概念
(1)若点![]() 是
是![]() 的等角点,且
的等角点,且![]() ,则
,则![]() 的度数是
的度数是 ![]() .
.
(2)已知点![]() 在
在![]() 的外部,且与点
的外部,且与点![]() 在
在![]() 的异侧,并满足
的异侧,并满足![]() ,作
,作![]() 的外接圆
的外接圆![]() ,连接
,连接![]() ,交圆
,交圆![]() 于点
于点![]() .当
.当![]() 的边满足下面的条件时,求证:
的边满足下面的条件时,求证:![]() 是
是![]() 的等角点.(要求:只选择其中一道题进行证明!)
的等角点.(要求:只选择其中一道题进行证明!)
①如图①,![]()
②如图②,![]()
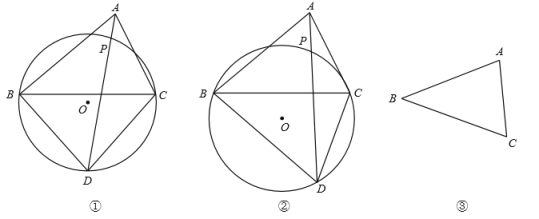
深入思考
(3)如图③,在![]() 中,
中,![]() 、
、![]() 、
、![]() 均小于
均小于![]() ,用直尺和圆规作它的强等角点
,用直尺和圆规作它的强等角点![]() .(不写作法,保留作图痕迹)
.(不写作法,保留作图痕迹)
(4)下列关于“等角点”、“强等角点”的说法:
①直角三角形的内心是它的等角点;
②等腰三角形的内心和外心都是它的等角点;
③正三角形的中心是它的强等角点;
④若一个三角形存在强等角点,则该点到三角形三个顶点的距离相等;
⑤若一个三角形存在强等角点,则该点是三角形内部到三个顶点距离之和最小的点,其中正确的有 .(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
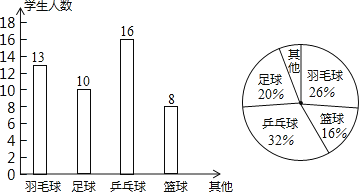
【题目】某校为了组织一次球类对抗赛,在本校随机抽取了若干名学生,对他们每个人最喜欢的一项球类运动进行了统计,将调查结果整理后绘制成如图所示的不完整的统计图,请你依据以上的信息回答下列问题:
(1)求本次被调查的学生人数;
(2)通过计算补全条形统计图;
(3)若全校有4000名学生,请你估计该校最喜欢篮球和足球运动的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=![]() ,求CD的长.
,求CD的长.
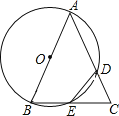
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(![]() ,3),B(
,3),B(![]() ,2),C(0,
,2),C(0,![]() ).
).
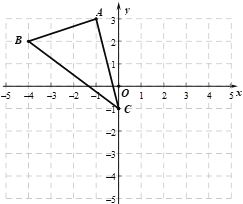
(1)以y轴为对称轴,把△ABC沿y轴翻折,画出翻折后的△![]() ;
;
(2)在(1)的基础上,
①以点C为旋转中心,把△![]() 顺时针旋转90°,画出旋转后的△
顺时针旋转90°,画出旋转后的△![]() ;
;
②点![]() 的坐标为 ,在旋转过程中点
的坐标为 ,在旋转过程中点![]() 经过的路径
经过的路径![]() 的长度为_____(结果保留π).
的长度为_____(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com