
分析 (1)方程组利用加减消元法求出解即可;
(2)原式利用零指数幂、负整数指数幂法则,以及特殊角的三角函数值计算即可得到结果.
解答 解:(1)$\left\{\begin{array}{l}{x+y=7①}\\{3x+y=17②}\end{array}\right.$,
②-①:2x=10,
解得:x=5,
把x=5代入①得:y=2,
则原方程组的解为:$\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$;
(2)原式=9-2×$\frac{\sqrt{2}}{2}$+1+$\sqrt{2}$=10.
点评 此题考查了解二元一次方程组,以及实数的运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
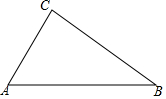 如图,在△ABC中,AB>AC.
如图,在△ABC中,AB>AC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,其中点B的坐标为(1,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是-1<k<$\frac{1}{4}$.
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,其中点B的坐标为(1,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是-1<k<$\frac{1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
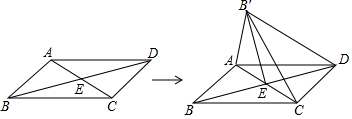
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
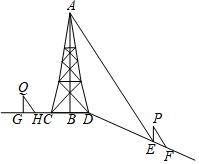 如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2m和1m.已知CD=12m,DE=18m,小明和小华身高均为1.6m,那么塔高AB为多少?
如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2m和1m.已知CD=12m,DE=18m,小明和小华身高均为1.6m,那么塔高AB为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com