
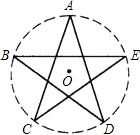
 如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )
如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )| A. | a•sin72° | B. | $\frac{a}{tan72°}$ | C. | $\frac{a}{cos18°}$ | D. | $\frac{a}{cos36°}$ |
分析 连AO,并延长交圆O于点F,连接CF.根据直径所对的圆周角是直角,得到直角三角形ACF.根据锐角三角函数进行求解.
解答 解:连AO,并延长交圆O于点F,连接CF,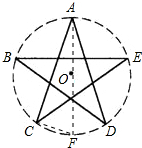
则∠ACF=90°;
∵A,B,C,D,E是圆O的五等分点.
∴∠CAD=∠DBE=∠ACE=∠ADB=∠BEC,
又∠CAD+∠DBE+∠ACE+∠ADB+∠BEC=180°,
∴∠CAD=$\frac{1}{5}$×180°=36°,
∴∠CAF=$\frac{1}{2}$∠CAD=18°,
在Rt△ACF中,AC=a,
∴AF=$\frac{AC}{cos∠CAF}$$\frac{a}{cos18°}$;
故选:C.
点评 本题考查了了圆周角定理的推论和正五边形的性质.熟练运用锐角三角函数进行求解是解决问题的关键.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:选择题
 在数学实践活动课中,小辉利用自己制作的一把“直角角尺”测量、计算一些圆的直径,如图,直角角尺,∠AOB=90°,将点O放在圆周上,分别确定OA、OB与圆的交点C、D,读得数据OC=8,OD=9,则此圆的直径约为( )
在数学实践活动课中,小辉利用自己制作的一把“直角角尺”测量、计算一些圆的直径,如图,直角角尺,∠AOB=90°,将点O放在圆周上,分别确定OA、OB与圆的交点C、D,读得数据OC=8,OD=9,则此圆的直径约为( )| A. | 17 | B. | 14 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
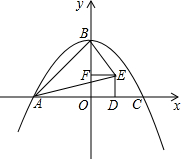 如图,二次函数y=-$\frac{1}{k}$x2+k(k>0)的图象与x轴相交于A、C两点(点A在点C的左侧),与y轴交于点B,点D为线段OC上一点(不与点O、C重合),以OD为边向上作正方形ODEF,连接AE,BE,AB,AB,设点D的横坐标为m.
如图,二次函数y=-$\frac{1}{k}$x2+k(k>0)的图象与x轴相交于A、C两点(点A在点C的左侧),与y轴交于点B,点D为线段OC上一点(不与点O、C重合),以OD为边向上作正方形ODEF,连接AE,BE,AB,AB,设点D的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
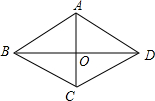 如图,在菱形ABCD中,点O是对角线的交点,|$\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{DO}$|:|$\overrightarrow{CB}+\overrightarrow{CD}+\overrightarrow{AO}$|=$\sqrt{3}$,求菱形ABCD的内角度数.
如图,在菱形ABCD中,点O是对角线的交点,|$\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{DO}$|:|$\overrightarrow{CB}+\overrightarrow{CD}+\overrightarrow{AO}$|=$\sqrt{3}$,求菱形ABCD的内角度数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
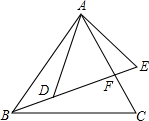 如图,点B、D、E在一条直线上,BE与AC相交于点F,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,若∠EAC=18°,则∠EBC=18°.
如图,点B、D、E在一条直线上,BE与AC相交于点F,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,若∠EAC=18°,则∠EBC=18°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com