
【题目】如图,已知△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,CE和BD交于点O,AO的延长线交BC于点F,则图中全等的三角形有( )

A.8对B.7对C.6对D.5对
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形![]() 的边长为
的边长为![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 在坐标轴上,把正方形
在坐标轴上,把正方形![]() 绕点
绕点![]() 顺时针旋转后得到正方形
顺时针旋转后得到正方形![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,且点
,且点![]() 恰为
恰为![]() 的中点,则点
的中点,则点![]() 的坐标为________.
的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校图书馆大楼工程在招标时,接到甲乙两个工程队的投标书,每施工一个月,需付甲工程队工程款16万元,付乙工程队12万元。工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:
(1)甲队单独完成此项工程刚好如期完工;
(2)乙队单独完成此项工程要比规定工期多用3个月;
(3)若甲乙两队合作2个月,剩下的工程由乙队独做也正好如期完工。
你觉得哪一种施工方案最节省工程款,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() ,则下列关于该函数的描述中,错误的是( )
,则下列关于该函数的描述中,错误的是( )
A. 该函数的最小值是![]()
B. 该函数图象与![]() 轴没有交点
轴没有交点
C. 该函数图象与![]() 轴有两个不同的交点
轴有两个不同的交点
D. 当![]() 时,
时,![]() 随着
随着![]() 的增大而增大
的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
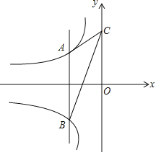
【题目】如图,动点![]() 在双曲线
在双曲线![]() 上,动点
上,动点![]() 在双曲线
在双曲线![]() 上,且直线
上,且直线![]() 轴,若点
轴,若点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .
.
![]() 当
当![]() 取不同的值时,
取不同的值时,![]() 的面积________(填“变化”或者“不变化”);
的面积________(填“变化”或者“不变化”);
![]() 线段
线段![]() 的长可以用
的长可以用![]() 表示为________;
表示为________;
![]() 若点
若点![]() 的坐标为
的坐标为![]() ,请问是否存在常数
,请问是否存在常数![]() ,使得
,使得![]() 的面积等于
的面积等于![]() ?若有,请求出
?若有,请求出![]() 的值;若没有,请说明理由.
的值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段BD.
(1)如图1,直接写出∠ABD的大小(用含α的式子表示);
(2)如图2,若∠BCE=150°,∠ABE=60°, ∠DEC=45°,求α的值;
(3)如图3,若∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某场足球比赛中,球员甲从球门底部中心点![]() 的正前方
的正前方![]() 处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为
处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为![]() 时达到最高点,此时足球飞行的水平距离为
时达到最高点,此时足球飞行的水平距离为![]() .已知球门的横梁高
.已知球门的横梁高![]() 为
为![]() .
.

![]() 在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
![]() 守门员乙站在距离球门
守门员乙站在距离球门![]() 处,他跳起时手的最大摸高为
处,他跳起时手的最大摸高为![]() ,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象与
的图象与![]() 轴正半轴交于
轴正半轴交于![]() 点.
点.

![]() 求证:该二次函数的图象与
求证:该二次函数的图象与![]() 轴必有两个交点;
轴必有两个交点;
![]() 设该二次函数的图象与
设该二次函数的图象与![]() 轴的两个交点中右侧的交点为点
轴的两个交点中右侧的交点为点![]() ,若
,若![]() ,将直线
,将直线![]() 向下平移
向下平移![]() 个单位得到直线
个单位得到直线![]() ,求直线
,求直线![]() 的解析式;
的解析式;
![]() 在
在![]() 的条件下,设
的条件下,设![]() 为二次函数图象上的一个动点,当
为二次函数图象上的一个动点,当![]() 时,点
时,点![]() 关于
关于![]() 轴的对称点都在直线
轴的对称点都在直线![]() 的下方,求
的下方,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com