
【题目】将矩形纸片放![]() 在平面直角坐标系中,
在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 是边
是边![]() 上的-一个动点,将
上的-一个动点,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处.
处.
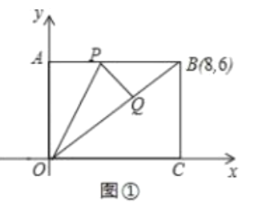
![]() 如图①.当点
如图①.当点![]() 恰好落在
恰好落在![]() 上时,求点
上时,求点![]() 的坐标;
的坐标;
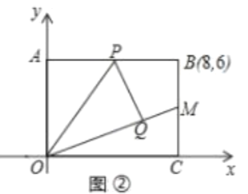
(2)如图②,当点![]() 是
是![]() 中点时,直线
中点时,直线![]() 交
交![]() 于
于![]() 点,
点,
![]() 求证:
求证:![]() ;
;
![]() 求点
求点![]() 的坐标.
的坐标.
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的解析式为
的解析式为![]() ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.![]() 确定抛物线的开口方向与大小
确定抛物线的开口方向与大小
B.若将抛物线![]() 沿
沿![]() 轴平移,则
轴平移,则![]() ,
,![]() 的值不变
的值不变
C.若将抛物线![]() 沿
沿![]() 轴平移,则
轴平移,则![]() 的值不变
的值不变
D.若将抛物线![]() 沿直线
沿直线![]() :
:![]() 平移,则
平移,则![]() 、
、![]() 、
、![]() 的值全变
的值全变
查看答案和解析>>
科目:初中数学 来源: 题型:
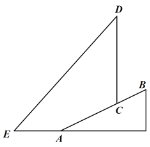
【题目】为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为多少米?(参考数据:sin48°≈0.73,cos48°≈0.67,tan48°≈1.11)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将
将![]() 折叠,得
折叠,得![]() .
.
(1)如图所示,当![]() 时,
时,![]() _______度;
_______度;

(2)如图所示,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;

(3)当点![]() 为
为![]() 中点时,点
中点时,点![]() 是边
是边![]() 上不与点
上不与点![]() 、
、![]() 重合的一个动点,将
重合的一个动点,将![]() 沿
沿![]() 折叠,得到
折叠,得到![]() ,连接
,连接![]() ,求
,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知A![]() ,B
,B![]() 是一次函数y=kx+b与反比例函数
是一次函数y=kx+b与反比例函数![]() 图象的两个交点.
图象的两个交点.

(1) 根据图象回答:当x满足 ,一次函数的值小于反比例函数的值;
(2) 将直线AB沿y轴方向,向下平移n个单位,与双曲线![]() 有唯一的公共点时,求n的值;
有唯一的公共点时,求n的值;
(3) 如图2,P点在![]() 的图象上,矩形OCPD的两边OD、OC在坐标轴上,且OC=2OD,M、N分别为OC、OD的中点,PN与DM交于点E,直接写出四边形EMON的面积为 .
的图象上,矩形OCPD的两边OD、OC在坐标轴上,且OC=2OD,M、N分别为OC、OD的中点,PN与DM交于点E,直接写出四边形EMON的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
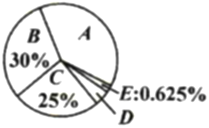
【题目】十九大召开后,某社区开展了“市民对十九大的关注情况”调查,采用随机抽样的方法访问了部分年龄在18周岁以上的城乡居民.小聪根据调查数据绘制了如下不完整的频数分布置表和扇形统计图.请根据图表解答下列问题.
关注情况 | 频数 |
非常关注( | 128 |
比较关注( | |
一般关注( | 80 |
不太关注( | |
不关注( | 2 |
(1)请完成频数分布表空格数据填写;
(2)求“非常关注”部分扇形圆心角的度数;
(3)若该社区18周岁以上居民共有20000人,请估计“比较关注”和“非常关注”的居民共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
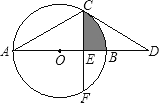
【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《小猪佩奇》这部动画片,估计同学们都非常喜欢.周末,小猪佩奇一家4口人(小猪佩奇,小猪乔治,小猪妈妈,小猪爸爸)到一家餐厅就餐,包厢有一圆桌,旁边有四个座位(![]() ,
,![]() ,
,![]() ,
,![]() ).
).


(1)小猪佩奇随机坐到![]() 座位的概率是________;
座位的概率是________;
(2)若现在由小猪佩奇,小猪乔治两人先后选座位,用树状图或列表的方法计算出小猪佩奇和小猪乔治坐对面的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com